题目内容
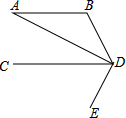 如图,已知AB∥CD,DA平分∠BDC,∠ADE=90°,∠B=120°,求∠BDE的度数.
如图,已知AB∥CD,DA平分∠BDC,∠ADE=90°,∠B=120°,求∠BDE的度数.考点:平行线的性质
专题:
分析:根据平行线的性质求出∠BDC,根据角平分线定义求出∠BDA,代入∠BDE=∠BDA+∠ADE求出即可.
解答:解:∵AB∥CD,∠B=120°,
∴∠BDC=180°-∠B=60°,
∵DA平分∠BDC,
∴∠BDA=∠ADC=
∠BDC=30°,
∵∠ADE=90°,
∴∠BDE=∠BDA+∠ADE=30°+90°=120°.
∴∠BDC=180°-∠B=60°,
∵DA平分∠BDC,
∴∠BDA=∠ADC=
| 1 |
| 2 |
∵∠ADE=90°,
∴∠BDE=∠BDA+∠ADE=30°+90°=120°.
点评:本题考查了平行线的性质和角平分线定义的应用,解此题的关键是求出∠BDC的度数,注意:两直线平行,同旁内角互补.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( )
如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( )| A、90° | B、135° |
| C、150° | D、120° |
直角坐标系中,点A(-3,4)与点B(-3,-4)关于( )
| A、原点中心对称 |
| B、y轴轴对称 |
| C、x轴轴对称 |
| D、以上都不对 |
 由一些相同的小正方体搭成的几何体的三视图如图所示,则搭成该几何体的小正方体有( )
由一些相同的小正方体搭成的几何体的三视图如图所示,则搭成该几何体的小正方体有( )| A、3个 | B、4个 | C、5个 | D、6个 |
某中学男子足球队21名同学的身高如下表
则这组身高数据的众数和中位数分别是( )
| 身高(cm) | 170 | 176 | 178 | 182 | 184 |
| 人数 | 3 | 7 | 5 | 3 | 3 |
| A、176,176 |
| B、176,177 |
| C、176,178 |
| D、184,178 |

 某校为了了解学生的身高情况,对部分学生的身高进行统计,根据身高(身高取整数,最高179cm,最矮155cm),分别绘制如下统计表和统计图.
某校为了了解学生的身高情况,对部分学生的身高进行统计,根据身高(身高取整数,最高179cm,最矮155cm),分别绘制如下统计表和统计图.