题目内容
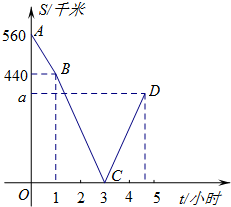甲乙两车分别从A、B两地相向而行，甲车比乙车先出发，出发后以各自的速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的距离S（千米）与甲车出发时间t（小时）之间的函数图象，其中D点表示甲车到达B地，停止行驶．有下列结论．其中，错误的结论是（ ）| A、A、B两地相距560千米 | ||
| B、乙车行驶速度为100 km/h | ||
C、a=
| ||
| D、t=2时，S=200千米 |
考点：一次函数的应用
专题：
分析：根据t=0时的S的值为A、B两地间的距离解答，再根据AB为甲车先行驶求出甲车的速度，设乙车的速度为vkm/h，根据相遇问题列方程求解即可得到乙车的速度，再求出甲车到达B地的时间，然后根据两车的速度列式计算即可求出a的值，根据两车的速度结合图形求出相遇前1小时的距离即为t=2时的S的值．
解答：解：t=0时，S=560，
所以，A、B两地相距560千米正确，
甲车的速度为（560-440）÷1=120km/h，
设乙车的速度为vkm/h，
则（120+v）×（3-1）=440，
解得v=100，
所以，乙车行驶速度为100km/h正确，
甲车到达B地的时间为560÷120=
小时，
a=（
-3）×（120+100）=
，
t=2时，S=（120+100）×（3-1）=220千米，
综上所述，结论错误的是t=2时，S=200千米．
故选D．
所以，A、B两地相距560千米正确，
甲车的速度为（560-440）÷1=120km/h，
设乙车的速度为vkm/h，
则（120+v）×（3-1）=440，
解得v=100，
所以，乙车行驶速度为100km/h正确，
甲车到达B地的时间为560÷120=
| 14 |
| 3 |
a=（
| 14 |
| 3 |
| 1100 |
| 3 |
t=2时，S=（120+100）×（3-1）=220千米，
综上所述，结论错误的是t=2时，S=200千米．
故选D．
点评：本题考查了一次函数的应用，主要利用了路程、速度、时间三者之间的关系，准确识图并理解各时间段两车的行驶过程是解题的关键．
练习册系列答案
相关题目
