题目内容
7.(1)解不等式组:$\left\{\begin{array}{l}{x-1>2x①}\\{\frac{x}{2}+3<-2②}\end{array}\right.$(2)化简:($\frac{{a}^{2}}{b}$-a)÷$\frac{{a}^{2}-{b}^{2}}{b}$.
分析 (1)先求出每个不等式的解集,再求出不等式组的解集即可;
(2)先算减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.
解答 解:(1)∵解不等式①得:x<-1,
解不等式②得:x<-10,
∴不等式组的解集为x<-10;
(2)原式=$\frac{{a}^{2}-ab}{b}$÷$\frac{(a+b)(a-b)}{b}$
=$\frac{a(a-b)}{b}$•$\frac{b}{(a+b)(a-b)}$
=$\frac{a}{a+b}$.
点评 本题考查了分式的混合运算和解一元一次不等式组,能根据不等式的解集找出不等式组的解集是解(1)的关键,能灵活运用分式的运算法则进行化简是解(2)的关键,注意运算顺序.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 数据1,2,3,2,5的中位数是3 | |
| B. | 对我市某社区每天丢弃塑料袋数量的调查,应采用普查的方式 | |
| C. | 在同一年出生的367名学生中,至少有两人的生日是同一天 | |
| D. | 若甲组数据的方差是0.15,乙组数据的方差是0.21,则乙组数据比甲组数据稳定 |
2.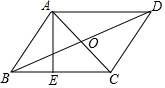 如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
 如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{21}}{7}$ | D. | $\frac{2\sqrt{21}}{7}$ |
12.9的算术平方根是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $\sqrt{3}$ |
 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.
如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.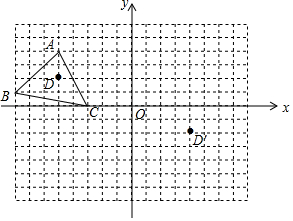 如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,
如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,