题目内容
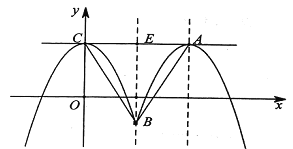
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() .
.
(Ⅰ)若抛物线![]() 经过原点,求
经过原点,求![]() 的值;
的值;
(Ⅱ)是否存在![]() 的值,使得点
的值,使得点![]() 到
到![]() 轴距离等于点
轴距离等于点![]() 到直线
到直线![]() 距离的一半,若存在,请直接写出
距离的一半,若存在,请直接写出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)将![]() 的函数图象记为图象
的函数图象记为图象![]() ,图象
,图象![]() 关于直线
关于直线![]() 的对称图象记为图象
的对称图象记为图象![]() ,图象
,图象![]() 与图象
与图象![]() 组合成的图象记为
组合成的图象记为![]() .
.
①当![]() 与
与![]() 轴恰好有三个交点时,求
轴恰好有三个交点时,求![]() 的值:
的值:
②当![]() 为等边三角形时,直接写出
为等边三角形时,直接写出![]() 所对应的函数值小于0时,自变量
所对应的函数值小于0时,自变量![]() 的取值范围.
的取值范围.
【答案】(1) m=![]() ;(2) m=2;(3)①m=
;(2) m=2;(3)①m=![]() ,②x<
,②x<![]() 或
或![]() 或x>
或x>![]()
【解析】
(1)将原点代入表达式,即可求出m;
(2)利用使得点![]() 到
到![]() 轴距离等于点
轴距离等于点![]() 到直线
到直线![]() 距离的一半,给出等量关系即可求出结果,
距离的一半,给出等量关系即可求出结果,
(3):①当![]() 与
与![]() 轴恰好有三个交点时,则抛物线与直线
轴恰好有三个交点时,则抛物线与直线![]() 相交于点
相交于点![]() 为(
为(![]() );
);
②,利用![]() 为等边三角形,算出m的值,然后求函数M的零点,即可给出答案,
为等边三角形,算出m的值,然后求函数M的零点,即可给出答案,
解:
(1)将原点代入表达式得0=-m+2,∵ m>0,∴m=![]() ;
;
(2) ![]() 时,
时,![]() ,B(
,B(![]() ,
,![]() ),
),
点A(m,2),则C(0,2),
点![]() 到直线
到直线![]() 距离为
距离为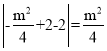
点![]() 到
到![]() 轴距离为
轴距离为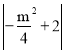 ,∴
,∴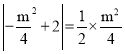 ,
,
∵ ![]() (舍)
(舍)![]() 或
或![]() 或
或![]() (舍).
(舍).
∴![]() 或
或![]() .
.
(3)①∵![]() 与
与![]() 轴恰好有三个交点,
轴恰好有三个交点,
∴抛物线与直线![]() 相交于点
相交于点![]() 为(
为(![]() ),将B代入表达式
),将B代入表达式![]() ,得
,得![]() ,则m=
,则m=![]() 或 m=
或 m=![]() (舍).
(舍).
②∵![]() 为等边三角形,AC=m,AC边上的高为B点到AC的距离,且长为
为等边三角形,AC=m,AC边上的高为B点到AC的距离,且长为![]()
可列方程![]() ,可得m=
,可得m=![]() (负值已舍),
(负值已舍),
当y=0时,![]() ,解得x=
,解得x=![]() ,
,
当y=0时, ![]() ,解得x=
,解得x=![]() ,∵
,∵![]() ,
,
∴B点在x轴下方,则此时M函数的小于0的范围为x<![]() 或
或![]() 或x>
或x>![]() .
.

练习册系列答案
相关题目