题目内容
18．
如图，△ABC在直角坐标系中的位置如图所示，点A的坐标为（1，2），若将△ABC绕点O旋转，点C的对应点为点D，则旋转后点A的对应点的坐标为（ ）| A． | （-1，2） | B． | （0，-1） | C． | （1，-3） | D． | （2，-1） |
分析 先根据点C的对应点为点D，得到旋转的方向与角度，再根据点A绕着点O顺时针旋转90°后的位置，得出旋转后点A的对应点的坐标．
解答 解：如图所示，连接CO，DO，则∠COD=90°，
∴点C绕着点O顺时针旋转90°与点D重合，
∴点A绕着点O顺时针旋转90°后落在点E处，
∵E（2，-1），
∴旋转后点A的对应点的坐标为（2，-1），
故选：D．
点评 本题主要考查了坐标与图形变化，解题时注意：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
9．下列计算错误的是（ ）
| A． | $\sqrt{\frac{4}{3}}$÷$\sqrt{\frac{1}{21}}$=2$\sqrt{7}$ | B． | （$\sqrt{8}$+$\sqrt{3}$）×$\sqrt{3}$=2$\sqrt{6}$+3 | C． | （4$\sqrt{2}$-3$\sqrt{6}$）÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ | D． | （$\sqrt{5}$+7）（$\sqrt{5}$-7）=-2 |
6．下列二次根式中，是最简二次根式的是（ ）
| A． | $\sqrt{15}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{5}}$ | D． | $\sqrt{9}$ |
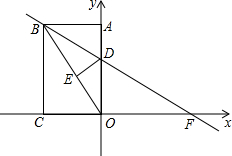如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（-6，8）．矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为（ ）
8．平面直角坐标系中，点P（m2+1，-1-n2）一定在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |