题目内容
如图，已知OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA=2，则PQ的最小值为________，理论根据为________．
2 角平分线上的点到角两边的距离相等
分析：过P作PQ⊥OM于Q，此时PQ的长最短，根据角平分线性质得出PQ=PA=2即可．
解答：
过P作PQ⊥OM于Q，此时PQ的长最短，
∵OP平分∠MON，PA⊥ON，PA=2，
∴PQ=PA=2（角平分线上的点到角两边的距离相等），
故答案为：2，角平分线上的点到角两边的距离相等．
点评：本题考查了角平分线性质，勾股定理的应用，注意：角平分线上的点到角两边的距离相等．
分析：过P作PQ⊥OM于Q，此时PQ的长最短，根据角平分线性质得出PQ=PA=2即可．
解答：
过P作PQ⊥OM于Q，此时PQ的长最短，
∵OP平分∠MON，PA⊥ON，PA=2，
∴PQ=PA=2（角平分线上的点到角两边的距离相等），
故答案为：2，角平分线上的点到角两边的距离相等．
点评：本题考查了角平分线性质，勾股定理的应用，注意：角平分线上的点到角两边的距离相等．
练习册系列答案
相关题目
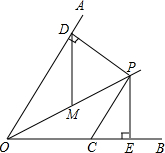（2013•西宁）如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（ ）
如图，已知OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA=2，则PQ的最小值为
，CP
，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是
B．
C．
D．
