题目内容
10.如图是小强用铜币摆放的4个图案,根据摆放图案的规律,试猜想第n个图案需要$\frac{1}{2}$n(n+1)+1个铜币.
分析 找出相邻两个图形铜币的数目的差,从而可发现其中的规律,于是可求得问题的答案.
解答 解:n=1时,铜币个数=1+1=2;
当n=2时,铜币个数=1+1+2=4;
当n=3时,铜币个数=1+1+2+3=7;
当n=4时,铜币个数=1+1+2+3+4=11;
…
第n个图案,铜币个数=1+1+2+3+4+…+n=$\frac{1}{2}$n(n+1)+1.
故答案为:$\frac{1}{2}$n(n+1)+1.
点评 本题主要考查的是图形的变化规律,找出其中的规律是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.今年,我市全面启动“精准扶贫”工作,某校为了了解九年级贫困生人数,对该校九年级6个班进行摸排,得到各班贫困生人数分别为12,12,14,10,18,16,这组数据的众数和中位数分别是( )
| A. | 12和10 | B. | 12和13 | C. | 12和12 | D. | 12和14 |
15.某校在国学文化进校园活动中,随机统计50名学生一周的课外阅读时间如表所示,这组数据的众数和中位数分别是( )
| 学生数(人) | 5 | 8 | 14 | 19 | 4 |
| 时间(小时) | 6 | 7 | 8 | 9 | 10 |
| A. | 14,9 | B. | 9,9 | C. | 9,8 | D. | 8,9 |
2.反比例函数y=-$\frac{1}{x}$的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( )
| A. | y1<y2<0 | B. | y1<0<y2 | C. | y1>y2>0 | D. | y1>0>y2 |
19.2100000用科学记数法表示应为( )
| A. | 0.21×108 | B. | 2.1×106 | C. | 2.1×107 | D. | 21×105 |
20.若m<n<0,那么下列结论错误的是( )
| A. | m-9<n-9 | B. | -m>-n | C. | $\frac{1}{n}>\frac{1}{m}$ | D. | 2m<2n |

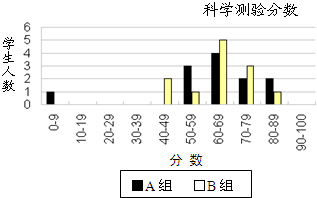 如图是两组学生参加科学测验的结果,这两组学生分别称为A组和B组.A组的平均分数是62.0分,B组的平均分数是64.5分.当学生得分为50分或以上时他们便通过这个测验.由图,老师认为B组学生比A组学生的表现好.但A组学生不同意老师的看法.他们说服老师B组学生并不一定好.依据上图,写出一个A组学生可能使用的数学论点是合格总人数A组多于B组.
如图是两组学生参加科学测验的结果,这两组学生分别称为A组和B组.A组的平均分数是62.0分,B组的平均分数是64.5分.当学生得分为50分或以上时他们便通过这个测验.由图,老师认为B组学生比A组学生的表现好.但A组学生不同意老师的看法.他们说服老师B组学生并不一定好.依据上图,写出一个A组学生可能使用的数学论点是合格总人数A组多于B组.