题目内容
在△ABC中，AB=AC=10，BC=12，则△ABC的面积为 ．
考点：勾股定理,等腰三角形的性质
专题：
分析：作底边上的高，构造直角三角形．运用等腰三角形性质及三角形的面积公式求解．
解答：
解：如图，作AD⊥BC于点D，则BD=
BC=6．
在Rt△ABD，
∵AD2=AB2-BD2，
∴AD=8，
∴△ABC的面积=
BC•AD=
×12×8=48．
故答案为：48．
解：如图，作AD⊥BC于点D，则BD=| 1 |
| 2 |
在Rt△ABD，
∵AD2=AB2-BD2，
∴AD=8，
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：48．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
一件服装的原价为a元，降价10%后的价格是（ ）
| A、10%a元 |
| B、10%元 |
| C、（1-10%）a元 |
| D、（1-10%a）元 |
计算（x2）3•（
x3-3x2+4x-1）÷（-x•x2）的结果为（ ）
| 1 |
| 2 |
A、
| ||
| B、-2x6+3x5-4x4-x3 | ||
C、-
| ||
| D、2x6-3x5-4x4+x3 |
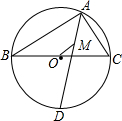如图，⊙O是△ABC的外接圆，BC为直径，AD平分∠BAC，交⊙O于D，点M是△ABC的内心．
如图，矩形纸片ABCD中，BC=m，将矩形的一角沿过点B的直线折叠，使点A落在DC边上，落点记为A′，折痕交AD于E，设∠A′BE=α．求证：EB=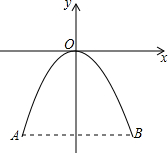
如图，一座抛物线形的拱桥，其形状可以用y=-x2来描述．