题目内容
 如图,△ABC中,AC=3,BC=4,AB=5,线段DE⊥AB,且△BDE的面积是△ABC面积的三分之一,那么,线段BD长为
如图,△ABC中,AC=3,BC=4,AB=5,线段DE⊥AB,且△BDE的面积是△ABC面积的三分之一,那么,线段BD长为考点:相似三角形的判定与性质,勾股定理的逆定理
专题:
分析:首先根据勾股定理的逆定理判断三角形ABC为直角三角形,再证明△ABC∽△EDB,利用相似三角形的性质即可求出线段BD长.
解答:解:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴三角形ABC为直角三角形,
∴∠C=90°,
∵DE⊥AB,
∴∠EDB=90°,
∴△ABC∽△EDB,
∴(
)2=
,
∵△BDE的面积是△ABC面积的三分之一,
∴BD=
,
故答案为
.
∴AC2+BC2=AB2,
∴三角形ABC为直角三角形,
∴∠C=90°,
∵DE⊥AB,
∴∠EDB=90°,
∴△ABC∽△EDB,
∴(
| BD |
| BC |
| S△BED |
| S△ABC |
∵△BDE的面积是△ABC面积的三分之一,
∴BD=
4
| ||
| 3 |
故答案为
4
| ||
| 3 |
点评:本题考查了勾股定理的逆定理和相似三角形的判断以及性质的运用,题目的综合性很好,难度不大.

练习册系列答案
相关题目
不等式x-2<0的解集在数轴上表示出来正确的是( )
A、 |
B、 |
C、 |
D、 |
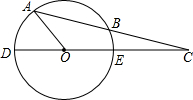 如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )
如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )| A、18° | B、22.5° |
| C、30° | D、15° |
下列四组数据不能组成直角三角形的是( )
| A、3,4,5 | ||||||
| B、6,8,10 | ||||||
| C、5,12,13 | ||||||
D、
|
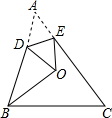 如图,△ABC中,O为三边垂直平分线的交点,将△ABC沿DE折叠,使顶点A恰好落在O点处,若BD=OB,则∠C的度数为( )
如图,△ABC中,O为三边垂直平分线的交点,将△ABC沿DE折叠,使顶点A恰好落在O点处,若BD=OB,则∠C的度数为( )| A、45° | B、54° |
| C、60° | D、72 |