Question

如图，梯形ABCD中，AD∥BC，且AD：BC=1：2，对角线AC、BD交于点O，那么S_△AOD：S_△BOC：S_△ABO=________．

Answer 1

1：4：2
分析：过A作AE垂直于OD，交OD于E，由AD与BC平行，得到两对内错角相等，由两对对应角相等的两三角形相似，得到三角形AOD与三角形COB相似，且相似比为AD：BC=1：2，进而得到两三角形的面积之比等于相似比得平方等于1：4，由三角形AOB与三角形AOD，高为同一条高，面积之比等于OD：OB也等于两相似三角形的相似比1：2，综上，求出三个三角形的面积之比．
解答：过A作AE⊥OD，交OD于E，

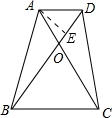
∵AD∥BC，
∴∠DAC=∠ACB，∠ADB=∠DBC，
∴△AOD∽△COB，
∵AD：BC=1：2，
∴S_△AOD：S_△BOC=1：4，OD：OB=1：2，
又∵S_△AOD=OD•AE，S_△AOB=OB•AE，
∴S_△AOD：S_△AOB==OD：OB=1：2，
则S_△AOD：S_△BOC：S_△ABO=1：4：2．
故答案为：1：4：2．
点评：此题考查了相似三角形的判定与性质，以及梯形的性质．相似三角形的对应边之比等于相似比，周长之比也等于相似比，面积之比等于相似比的平方．本题在探索三角形AOB与三角形AOD面积之比时，关键是作出公共高AE，根据三角形的面积公式分别表示出两三角形的面积，约分后得到两三角形面积之比等于两对边之比．