Ő‚ńŅńŕ»›
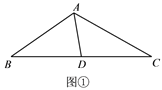
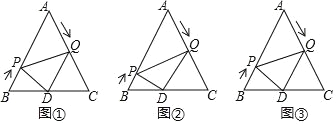
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™°ųABC «ĪŖ≥§ő™6cmĶńĶ»ĪŖ»żĹ«–ő£¨∂ĮĶ„P£¨QÕ¨ Īī”B£¨AŃĹĶ„≥Ų∑Ę£¨∑÷Īū—ōBA£¨AC‘»ňŔ‘ň∂Į£¨∆š÷–Ķ„P‘ň∂ĮĶńňŔ∂» «1cm/s£¨Ķ„Q‘ň∂ĮĶńňŔ∂» «2cm/s£¨ĶĪĶ„QĶĹīÔĶ„C Ī£¨P£¨QŃĹĶ„∂ľÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™t£®s£©£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©»ÁÕľĘŔ£¨ĶĪtő™ļő÷Ķ Ī£¨AP£Ĺ3AQ£Ľ
£®2£©»ÁÕľĘŕ£¨ĶĪtő™ļő÷Ķ Ī£¨°ųAPQő™÷ĪĹ«»żĹ«–ő£Ľ
£®3£©»ÁÕľĘŘ£¨◊ų QD°őABĹĽ BC”ŕĶ„D£¨Ń¨Ĺ”PD£¨ĶĪtő™ļő÷Ķ Ī£¨°ųBDP”Ž°ųPDQŌŗň∆£Ņ
°ĺīūįł°Ņ£®1£©![]() £®2£©3ĽÚ
£®2£©3ĽÚ![]() £®3£©
£®3£©![]() ĽÚ2
ĽÚ2
°ĺĹ‚őŲ°Ņ
(1)”…Ő‚“‚Ņ…÷™BP=t,AQ=2t,‘ÚAP=6-t”…AP=3AQŅ…Ķ√ĶĹĻō”ŕtĶń∑Ĺ≥Ő,Ņ…«ůĶ√Ķń÷Ķ;
(2)∑÷°ŌAPQ=90![]() ļÕ¶§AQP=90
ļÕ¶§AQP=90![]() ŃĹ÷÷«ťŅŲ,‘ŔņŻ”√ļ¨30Ĺ«Ķń÷ĪĹ«»żĹ«–őĶń–‘÷ Ņ…ļÕAP=2AQ,ĽÚAQ=2AP,∑÷Īū«ůľīŅ…;
ŃĹ÷÷«ťŅŲ,‘ŔņŻ”√ļ¨30Ĺ«Ķń÷ĪĹ«»żĹ«–őĶń–‘÷ Ņ…ļÕAP=2AQ,ĽÚAQ=2AP,∑÷Īū«ůľīŅ…;
(3) ”…“—÷™Ņ…÷§Ķ√°ųCDQ «Ķ»ĪŖ»żĹ«–ő£¨∑÷°ųBPD°◊°ųPDQ £¨°ųBPQ °◊°ųQDP ŃĹ÷÷«ťŅŲŐ÷¬Ř£¨Ņ…Ķ√tĶń÷Ķ.
£®1£©”…Ő‚“‚÷™£¨AQ£Ĺ2t£¨BP£Ĺt£¨
°Ŗ°ųABC «ĪŖ≥§ő™ 6cm ĶńĶ»ĪŖ»żĹ«–ő£¨
°ŗ°ŌA£Ĺ60°„£¨AB£Ĺ6£¨
°ŗAP£ĹAB©ĀBP£Ĺ6©Āt£¨
°ŖAP£Ĺ3AQ£¨
°ŗ6©Āt£Ĺ3°Ń2t£¨
°ŗt£Ĺ![]() £¨
£¨
ľī£ļt£Ĺ![]() √Ž Ī£¨AP£Ĺ3AQ£Ľ
√Ž Ī£¨AP£Ĺ3AQ£Ľ
£®2£©”…£®1£©÷™£¨°ŌA£Ĺ60°„£¨AQ£Ĺ2t£¨AP£Ĺ6©Āt£¨
°Ŗ°ųAPQ ő™÷ĪĹ«»żĹ«–ő£¨
ĘŔĶĪ°ŌAPQ£Ĺ90°„ Ī£¨AQ£Ĺ2AP£¨
°ŗ2t£Ĺ2£®6©Āt£©£¨
°ŗt£Ĺ3 √Ž£¨
ĘŕĶĪ°ŌAQP£Ĺ90°„ Ī£¨AP£Ĺ2AQ£¨
°ŗ6©Āt£Ĺ2°Ń2t£¨
°ŗt£Ĺ![]() √Ž£¨
√Ž£¨
ľī£ļt£Ĺ3 √ŽĽÚ![]() √Ž Ī£¨°ųAPQ «÷ĪĹ«»żĹ«–ő£Ľ
√Ž Ī£¨°ųAPQ «÷ĪĹ«»żĹ«–ő£Ľ
£®3£©”…Ő‚“‚÷™£¨AQ£Ĺ2t£¨BP£Ĺt£¨
°ŗAP£Ĺ6©Āt£¨
°Ŗ°ųABC «Ķ»ĪŖ»żĹ«–ő£¨
°ŗ°ŌA£Ĺ°ŌC£Ĺ60°„£¨
°ŖQD°őAB£¨
°ŗ°ŌPDQ£Ĺ°ŌBPD£¨°ŌQDB£Ĺ°ŌA£Ĺ60°„£¨
°ŗ°ųCDQ «Ķ»ĪŖ»żĹ«–ő£¨
°ŗCD£ĹCQ£¨
°ŗBD£ĹAQ£Ĺ2t£¨
°Ŗ°ųBDP ”Ž°ųPDQ Ōŗň∆£¨
°ŗĘŔĶĪ°ųBPD°◊°ųPDQ Ī£¨
°ŗ°ŌB£Ĺ°ŌDPQ£Ĺ60°„£¨
°ŗ°ŌAPQ£Ĺ°ŌBDP£¨
°Ŗ°ŌA£Ĺ°ŌB£¨
°ŗ°ųAPQ°◊°ųBDP£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗt£Ĺ![]() √Ž£¨
√Ž£¨
ĘŕĶĪ°ųBPQ °◊°ųQDP Ī£¨
°ŗ°ŌB£Ĺ°ŌDQP£Ĺ60°„£¨
°ŖDQ°őAB£¨
°ŗ°ŌAPQ£ĹDQP£Ĺ60°„£¨
°Ŗ°ŌA£Ĺ60°„£¨
°ŗ°ųAPQ «Ķ»ĪŖ»żĹ«–ő£¨
°ŗAP£ĹAQ£¨
°ŗ6©Āt£Ĺ2t£¨
°ŗt£Ĺ2 √Ž£¨
ľī£ļt£Ĺ![]() √ŽĽÚ 2 √Ž Ī£¨°ųBDP ”Ž°ųPDQ Ōŗň∆£ģ
√ŽĽÚ 2 √Ž Ī£¨°ųBDP ”Ž°ųPDQ Ōŗň∆£ģ