Question

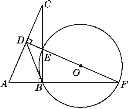
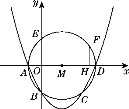
【题目】如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c与⊙M相交于A、B、C、D四点，其中A、B两点的坐标分别为(－1，0)，(0，－2)，点D在x轴上且AD为⊙M的直径．点E是⊙M与y轴的另一个交点，过劣弧ED上的点F作FH⊥AD于点H，且FH＝1.5.

(1)求点D的坐标及该抛物线对应的函数表达式；

(2)若点P是x轴上的一个动点，试求出△PEF的周长最小时点P的坐标.

Answer 1

【答案】（1）D（4，0），y=x2－x－2；（2）P(2，0)．

【解析】

（1）首先根据圆的轴对称性求出点D的坐标，将A、B、D三点代入，即可求出本题的答案；

（2）由于点E与点B关于x轴对称，所以，连接BF，直线BF与x轴的交点，即为点P，据此即可得解．

（1）连接BD．

∵AD是⊙M的直径，∴∠ABD=90°，∴△AOB∽△ABD，∴．在Rt△AOB中，AO=1，BO=2，根据勾股定理得：AB，∴，∴AD=5，∴DO=AD﹣AO=5﹣1=4，∴D（4，0），把点A（﹣1，0）、B（0，﹣2）、D（4，0）代入y=ax2+bx+c可得：

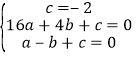，解得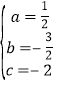：，∴抛物线表达式为：；

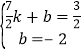（2）连接FM．在Rt△FHM中，FM，FH，∴MH2，OM=AM﹣OA，∴OH=OM+MH，∴F（），设直线BF的解析式为y=kx+b，则：，∴直线BF的解析式为：y=x﹣2，连接BF交x轴于点P．

∵点E与点B关于x轴对称，∴点P即为所求，当y=0时，x=2，∴P（2，0）．