Question

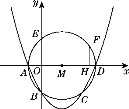
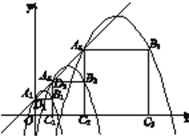
【题目】在平面直角坐标系xOy中，正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…，按如图的方式放置．点A1，A2，A3，…，An和点C1，C2，C3，…，Cn分别落在直线y＝x＋1和x轴上．抛物线L1过点A1，B1，且顶点在直线y＝x＋1上，抛物线L2过点A2，B2，且顶点在直线y＝x＋1上，…，按此规律，抛物线Ln过点An，Bn，且顶点也在直线y＝x＋1上，其中抛物线L2交正方形A1B1C1O的边A1B1于点D1，抛物线L3交正方形A2B2C2C1的边A2B2于点D2，…，抛物线Ln＋1交正方形AnBnCnCn－1的边AnBn于点Dn(其中n≥2且n为正整数)．

(1)直接写出下列点的坐标：B1________，B2________，B3________；

(2)写出抛物线L2、L3的解析式，并写出其中一个解析式求解过程，再猜想抛物线Ln的顶点坐标

(3)设A1D1＝k1·D1B1，A2D2＝k2·D2B2，试判断k1与k2的数量关系并说明理由．

Answer 1

【答案】(1)B1(1，1)，B2(3，2)，B3(7，4).（2）（， ）；（3）k1＝k2

【解析】试题解析：（1）由直线解析式可求得A1的坐标，由正方形的性质则可求得B1坐标，由题意可求得A2的横坐标，则可求得其纵坐标，再利用正方形的性质可求得B2的坐标，同理可求得B3的坐标；

（2）由对称性可求得抛物线的对称轴，则可求得其顶点坐标，再结合已知点的坐标可求得抛物线解析式，可写出L2、L3的解析式；利用An、Bn的变化规律，可求得抛物线Ln的顶点坐标；

（3）由抛物线L2的解析式可求得A1D1的长，则可求得k1，同理可求得k2，从而可求得两者之间的数量关系．

试题解析：解：

（1）∵A1在直线y=x+1上，∴A1的坐标为（0，1），∴A1B1=OA1=1，∴B1（1，1），∴A2横坐标为1，且在直线y=x+1上，∴A2（1，2），∴A2B2=A2C1=2，∴B2（3，2），同理B3（7，4），故答案为：（1，1）；（3，2）；（7，4）；

（2）抛物线L2、L3的解析式分别为y=﹣（x﹣2）2+3，y=﹣（x﹣5）2+6；

抛物线L2的解析式的求解过程如下：

对于直线y=x+1，设x=0，可得y=1，∴A1（0，1），∵四边形A1B1C1O是正方形，∴C1（1，0），又点A2在直线y=x+1上，∴可得点A2（1，2），又∵B2的坐标为（3，2），∴抛物线L2的对称轴为直线x=2，∴抛物线L2的顶点为（2，3），设抛物线L2的解析式为：y=a（x﹣2）2+3，∵L2过点B2（3，2），∴2=a×（3﹣2）2+3，解得a=﹣1，∴抛物线L2的解析式为y=﹣（x﹣2）2+3；

猜想抛物线Ln的顶点坐标为（3×2n﹣2﹣1，3×2n﹣2）．

证明如下：

由正方形AnBnCnCn﹣1顶点An，Bn的坐标规律为An（2n﹣1﹣1，2n﹣1）与Bn（2n﹣1，2n﹣1），∴抛物线Ln的对称轴为直线x= =3×2n﹣2﹣1，又顶点在直线y=x+1上，∴y=3×2n﹣2，∴抛物线Ln的顶点坐标为（3×2n﹣2﹣1，3×2n﹣2）；

（3）k1与k2的数量关系为k1=k2．

理由如下：

由（2）得L2的解析式为y=﹣（x﹣2）2+3，当y=1时，1=﹣（x﹣2）2+3，解得x1= ，x2= ，∵0＜A1D1＜1，∴x=，∴A1D1== ，∴D1B1=1﹣（）= ，∴A1D1= D1B1，即k1=；

同理可求得A2D2= =，D2B2=2﹣（4﹣2 ）=2 ﹣2=2（），∴A2D2=D2B2，即k2=，∴k1=k2．