题目内容
三角形内角和定理的证明．
已知：如图所示，E是BC上一点，DE∥AC，EF∥AB．
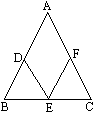
求证：∠A＋∠B＋∠C＝
．
证明：∵DE∥AC(已知)，
∴∠A＝________，∠C＝________( )．
∵EF∥AB(已知)，
∴________＝∠DEF( )，
∠B＝______( )．
∴∠A＝∠DEF( )．
∵BEC是直线(已知)，
∴∠BEC＝( )，
即∠DEF＋∠FEC＋∠DEB＝
，
∴∠A＋∠B＋∠C＝
( )．
答案：
解析：
解析：
|
∠BDE,∠BED,两直线平行，同位角相等,∠EDB,两直线平行，内错角相等,∠CEF,两直线平行，同位角相等,等量代换,平角定义,等量代换 |
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
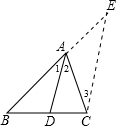E∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明
[]
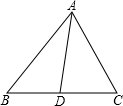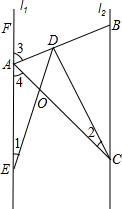说理，填空（在括号中填上相应的依据）
加上第三个角的一半.如图所示，△ABC中，若BD，CD分别是它的角平分线，则∠BDC＝
∠A
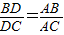
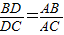，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似．现在B、D、C在一直线上，△ABD与△ADC不相似，需要考虑用别的方法换比．在比例式
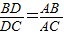中，AC恰是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明
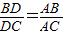就可以转化成证AE=AC．
，
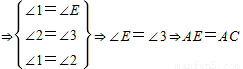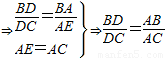
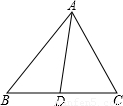
，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似．现在B、D、C在一直线上，△ABD与△ADC不相似，需要考虑用别的方法换比．在比例式
中，AC恰是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明
就可以转化成证AE=AC．
，
