Question

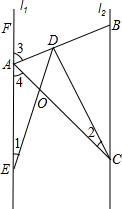
说理，填空（在括号中填上相应的依据）
已知：l₁∥l₂，∠CAB=∠CBA，∠ACB=∠CDE
求证：AB平分∠CAF；∠1=∠2．
证明如下：
∵l₁∥l₂（已知）
∴∠CBA=∠3（

两直线平行，内错角相等

）
∵∠CAB=∠CBA（已知）
∴∠3=∠CAB
∴AB平分∠CAF（

角平分线定义

）
∵l₁∥l₂（已知）
∴∠ACB=∠4（

两直线平行，内错角相等

）
又∵∠ACB=∠CDE（已知）
∴∠4=∠CDE（

等量代换

）
又∵∠4+∠1+∠AOE=180°
∠2+∠CDE+∠DOC=180°（

三角形内角和定理

）
∴∠4+∠1+∠AOE=∠2+∠CDE+∠DOC（

等量代换

）
∵∠4=∠CDE（已证），∠AOE=∠DOC（

已证

）
∴∠1=∠2．

Answer 1

分析：根据平行线的性质和三角形内角和定理推出即可．

解答：证明：∵l₁∥l₂，
∴∠CBA=∠3（两直线平行，内错角相等），
∵∠CAB=∠CBA，
∴∠3=∠CAB（等量代换），
∴AB平分∠CAF（角平分线定义），
∵l₁∥l₂，
∴∠ACB=∠4（两直线平行，内错角相等），
∵∠ACB=∠CDE
∴∠4=∠CDE（等量代换），
∵∠4+∠1+∠AOE=180°，∠2+∠CDE+∠DOC=180°（三角形内角和定理），
∴∠4+∠1+∠AOE=∠2+∠CDE+∠DOC（等量代换），
∵∠4=∠CDE，∠AOE=∠DOC（对顶角相等），
∴∠1=∠2，
故答案为：两直线平行，内错角相等，角平分线定义，两直线平行，内错角相等，等量代换，三角形内角和定理，等量代换，已证．

点评：本题考查了平行线性质，三角形内角和定理的应用，主要考查学生的推理能力．