题目内容
如图，一个圆锥侧面沿母线AC展开后正好是一个半圆，该圆锥的高OA和底面半径OC的数量关系是
- A.OA=OC
- B.OA=1.5OC
- C.OA=2OC
- D.
D
分析：根据圆锥的底面周长等于侧面展开图的弧长得到圆锥的母线长和底面半径的关系，即可得到∠ACO的度数，也就求得了圆锥的高OA和底面半径OC的数量关系．
解答：设圆锥的底面半径为r，母线长为R，
πR=2πr，
∴R=2r，
∴cos∠ACO=60°，
∴OA=
OC，
故选D．
点评：考查有关圆锥的计算；用到的知识点为：圆锥的底面周长等于侧面展开图的弧长；关键是得到∠ACO的度数．
分析：根据圆锥的底面周长等于侧面展开图的弧长得到圆锥的母线长和底面半径的关系，即可得到∠ACO的度数，也就求得了圆锥的高OA和底面半径OC的数量关系．
解答：设圆锥的底面半径为r，母线长为R，
πR=2πr，
∴R=2r，
∴cos∠ACO=60°，
∴OA=
OC，故选D．
点评：考查有关圆锥的计算；用到的知识点为：圆锥的底面周长等于侧面展开图的弧长；关键是得到∠ACO的度数．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
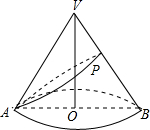如图是一个圆锥，它的高为
如图，一个圆锥侧面沿母线AC展开后正好是一个半圆，该圆锥的高OA和底面半径OC的数量关系是（ ）| A、OA=OC | ||
| B、OA=1.5OC | ||
| C、OA=2OC | ||
D、OA=
|
，母线长为6，A是底面圆周上的定点，动点P从A点出发，沿圆锥的侧面运动一周后仍回到A点，则点P经过路线的长度的最小值为 ．
