题目内容
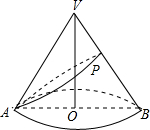 如图是一个圆锥,它的高为4
如图是一个圆锥,它的高为4| 2 |
分析:易得圆锥的底面周长也就是圆锥的侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角,进而构造等腰三角形求得相应线段即可.
解答: 解:∵一个圆锥,它的高为4
解:∵一个圆锥,它的高为4
,母线长为6,
∴底面圆的半径为:
=2,
圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.
∴
=4π,
解得n=120°,
∴∠AVD=120°,
∴∠A=30°,
∵AV=6,
∴VE=3,
AE=3
,
∴AD=6
,
∴最短路程为:6
.
故答案为:6
.
 解:∵一个圆锥,它的高为4
解:∵一个圆锥,它的高为4| 2 |
∴底面圆的半径为:
62-(4
|
圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.
∴
| nπ×6 |
| 180 |
解得n=120°,
∴∠AVD=120°,
∴∠A=30°,
∵AV=6,
∴VE=3,
AE=3
| 3 |
∴AD=6
| 3 |
∴最短路程为:6
| 3 |
故答案为:6
| 3 |
点评:此题主要考查了圆锥的有关计算以及平面展开图最短路径问题,求立体图形中两点之间的最短路线长,一般应放在平面内,构造三角形,求两点之间的线段的长度.用到的知识点为:圆锥的弧长等于底面周长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
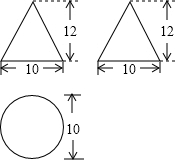 如图是一个圆锥的三视图,求它的母线长和侧面积.(结果保留π)
如图是一个圆锥的三视图,求它的母线长和侧面积.(结果保留π) 如图是一个圆锥,它的高为
如图是一个圆锥,它的高为 ,母线长为6,A是底面圆周上的定点,动点P从A点出发,沿圆锥的侧面运动一周后仍回到A点,则点P经过路线的长度的最小值为________.
,母线长为6,A是底面圆周上的定点,动点P从A点出发,沿圆锥的侧面运动一周后仍回到A点,则点P经过路线的长度的最小值为________. 如图是一个圆锥的三视图,求它的母线长和侧面积.(结果保留π)
如图是一个圆锥的三视图,求它的母线长和侧面积.(结果保留π) ,母线长为6,A是底面圆周上的定点,动点P从A点出发,沿圆锥的侧面运动一周后仍回到A点,则点P经过路线的长度的最小值为 .
,母线长为6,A是底面圆周上的定点,动点P从A点出发,沿圆锥的侧面运动一周后仍回到A点,则点P经过路线的长度的最小值为 .