题目内容
如图4361，在梯形ABCD中，AD∥BC，E为BC的中点，BC＝2AD，EA＝ED，AC与ED相交于点F.求证：梯形ABCD是等腰梯形．
证明：∵AD∥BC，
∴∠DEC＝∠EDA，∠BEA＝∠EAD.
又∵EA＝ED，
∴∠EAD＝∠EDA.∴∠DEC＝∠AEB.
又∵EB＝EC，
∴△DEC≌△AEB.∴AB＝CD.
∴梯形ABCD是等腰梯形．
练习册系列答案
阅读快车系列答案
相关题目
；③二次函数y＝(x－x1)(x－x2)＋m的图象与x轴交点的坐标为(2,0)和(3,0)．
青少年“心理健康”问题越来越引起社会的关注，某中学为了解学校600名学生的心理健康状况，举行了一次“心理健康”知识测试，并随机抽取了部分学生的成绩(得分取正整数，满分为100分)作为样本，绘制了下面未完成的频率分布表和频率分布直方图(如图7110)．请回答下列问题：
| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 14 | 0.28 |
| 70.5～80.5 | 16 | |
| 80.5～90.5 | ||
| 90.5～100.5 | 10 | 0.20 |
| 合计 | 1.00 |
图7110
(1)填写频率分布表中的空格，并补全频率分布直方图；
(2)若成绩在70分以上(不含70分)为心理健康状况良好，同时，若心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导．请根据上述数据分析该校学生是否需要加强心理辅导，并说明理由．
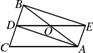
是一元一次不等式，则m=______。