题目内容
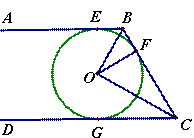
如图(1),AB、BC、CD分别与⊙O相切于点E、F、G,且AB∥CD, 若![]() ,
,
(1)求BC和OF的长;
(2)求证:![]() 三点共线;
三点共线;
(3)小叶从第(1)小题的计算中发现:等式
![]() 成立,于是她得到这样的结论:
成立,于是她得到这样的结论:
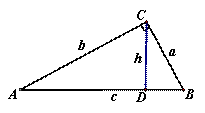
如图(2),在![]() 中,
中,![]() ,
,![]() ,
,
垂足为![]() ,设
,设![]() ,
,![]() ,则有等式
,则有等式
![]() 成立.请你判断小叶的结论是否正确,
成立.请你判断小叶的结论是否正确,
若正确,请给予证明,若不正确,请说明理由.
 | |||
 | |||
(1)解:
∵AB∥CD
∴∠ABC+∠BCD=180°
又∵AB,BC,CD分别与⊙O相切于点E,F,G
∴BO,CO分别平分∠ABC,∠BCD
∴∠OBC+∠OCB=90°
又∵在Rt△ABC中,∠BOC=90°,OB=6,OC=8
∴![]()
∴![]()
即:10×OF=6×8
∴OF=4.8-
(2)
证法一:连接OE,OG
∵BO分别平分∠ABC
∴∠EBO=∠FBO
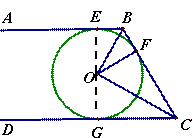 又∵AB,BC分别与⊙O相切于点E,F
又∵AB,BC分别与⊙O相切于点E,F
∴∠BEO=∠BFO=90°
∴∠BOE=∠BOF
同理:∠COG=∠COF
∵∠OBC+∠OCB=90°
∴∠EOG=∠EOB+∠BOF+∠COF+∠COG=180°
∴![]() 三点共线
三点共线
证法二:连接OE,OG
∵AB,BC,CD分别与⊙O相切于点E,F,G
∴∠BFO=∠BEO=∠OGC=90°
∴在四边形OEBF中,∠EBF+∠EOF=180°
同理:∠GCF+∠GOF=180°
∴∠EBF+∠EOF+∠GCF+∠GOF=360°
又∵AB∥CD
∴∠EBF+∠GCF=180°
∴∠EOF+∠GOF=180°
即:![]() 三点共线
三点共线
(3)
等式![]() 成立.理由如下:
成立.理由如下:
证法一:∵![]() ,
,![]() ,∠A为公共角
,∠A为公共角
∴△ACD∽△ABC
 ∴
∴![]()
∴![]()
∴![]()
同理![]() ,
,
![]()
∴![]()
∴![]()
证法二:tan∠CAB=![]()
∴![]()
∴![]() ∴
∴![]()
∴![]()
证法三∵![]()
∴![]()
∴![]() , ∴
, ∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 6、如图所示,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=20°,则∠EOF=
6、如图所示,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=20°,则∠EOF=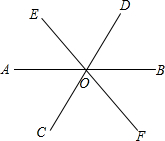 如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF=60°,求∠BOD的度数.
如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF=60°,求∠BOD的度数.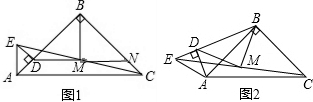
 22、(初三)如图,△ABC中,AB=AC,I为△ABC的内心,AI的延长线交△ABC的外接圆于点D,过点I作BC的平行线分别交AB、AC于E、F,若O是△DEF外接圆的圆心.
22、(初三)如图,△ABC中,AB=AC,I为△ABC的内心,AI的延长线交△ABC的外接圆于点D,过点I作BC的平行线分别交AB、AC于E、F,若O是△DEF外接圆的圆心.
 (1)解不等式组:
(1)解不等式组: