题目内容
袋中有6个球(除颜色不同外,其它完全相同),其中白球3个,红球2个,黑球1个,如果从中随机摸出2个球,那么这两个均为白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:列表是找出所有等可能的结果数,进而得出两次颜色不同的情况数,即可求出所求的概率.
解答:解:列表如下:
所有等可能结果数为30种,其中两个球均为白球的情况数有6种,
则概率P=
=
.
故选C.
| 白 | 白 | 白 | 红 | 红 | 黑 | |
| 白 | 白白 | 白白 | 红白 | 红白 | 黑白 | |
| 白 | 白白 | 白白 | 红白 | 红白 | 黑白 | |
| 白 | 白白 | 白白 | 红白 | 红白 | 黑白 | |
| 红 | 白红 | 白红 | 白红 | 红红 | 黑红 | |
| 红 | 白红 | 白红 | 白红 | 红红 | 黑红 | |
| 黑 | 白红 | 白红 | 白黑 | 红黑 | 红黑 |
则概率P=
| 6 |
| 30 |
| 1 |
| 5 |
故选C.
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知甲数比乙数的2倍少1.设乙数为x,用关于x的代数式表示甲数是( )
| A、2x+1 | ||
| B、2x-1 | ||
C、
| ||
D、
|
下列命题中是假命题的是( )
| A、同旁内角互补,两直线平行 |
| B、垂线段最短 |
| C、在同一平面内,过一点有且只有一条直线与已知直线垂直 |
| D、直线外一点到这条直线的垂线段叫做点到直线的距离 |
 如图,哪个可以通过左边图形平移得到( )
如图,哪个可以通过左边图形平移得到( )A、 |
B、 |
C、 |
D、 |
如果等式(
)2=x成立,那么x为( )
| -x |
| A、x≤0 | B、x=0 |
| C、x<0 | D、x≥0 |
下列运算正确的是( )
| A、5a-3a=2 |
| B、a2+a2=2a4 |
| C、3a2-2a2=a2 |
| D、-2(a-1)=-2a-1 |
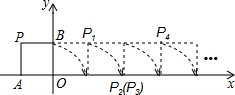 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2014次,点P依次落在点P1,P2,P3,…P2013,P2014的位置,记Pi(xi,yi),i=1,2,3,…,2013,2014,则P2014的坐标
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2014次,点P依次落在点P1,P2,P3,…P2013,P2014的位置,记Pi(xi,yi),i=1,2,3,…,2013,2014,则P2014的坐标