ЬтФПФкШн
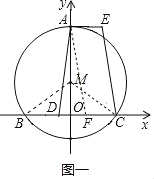
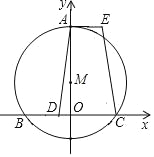
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌвдMЮЊдВаФЃЌвд4ЮЊАыОЖЕФдВгыxжсЯрНЛгкЕуBЁЂCЃЌгыyжсе§АыжсЯрНЛгкЕуAЙ§AзїAEЁЮBCЃЌЕуDЮЊЯвBCЩЯвЛЕуЃЌAEЃНBDЃЌСЌНгADЃЌECЃЎ
(1)ЧѓBЁЂCСНЕуЕФзјБъЃЛ
(2)ЧѓжЄЃКADЃНCEЃЛ
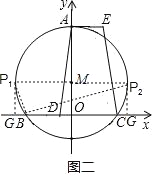
(3)ШєЕуPЪЧЛЁBACЩЯвЛЖЏЕу(PЕугыAЁЂBЕуВЛжиКЯ)ЃЌЙ§ЕуPЕФЁбMЕФЧаЯпPGНЛxжсгкЕуGЃЌШєЁїBPGЮЊжБНЧШ§НЧаЮЃЌЪдЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ
ЁОД№АИЁП(1)ЕуBЕФзјБъЮЊ(Љ2![]() ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2
ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2![]() ЃЌ0)ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2
ЃЌ0)ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2![]() ЃЌ4)ЃЌ(2
ЃЌ4)ЃЌ(2![]() ЃЌ4)ЃЎ
ЃЌ4)ЃЎ
ЁОНтЮіЁП
(1)ИљОнЙДЙЩЖЈРэПЩвдЧѓЕУOBКЭOCЕФГЄЖШЃЌДгЖјПЩвдЕУЕНBЁЂCСНЕуЕФзјБъЃЛ
(2)ИљОнЦНааЫФБпаЮЕФаджЪЁЂШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪПЩвджЄУїНсТлГЩСЂЃЛ
(3)ИљОнЬтвтЃЌЛГіЯргІЕФЭМаЮЃЌШЛКѓРћгУЗжРрЬжТлЕФЗНЗЈПЩвдЕУЕНЕуPЕФзјБъЃЎ
НтЃК(1)СЌНгMBЁЂMCЃЌШчЭМвЛЫљЪОЃЌ
ЁпЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌвдMЮЊдВаФЃЌвд4ЮЊАыОЖЕФдВгыxжсЯрНЛгкЕуBЁЂCЃЌ
ЁрMBЃНMCЃН4ЃЌOMЃН2ЃЌ
ЁпЁЯMOBЃНЁЯMOCЃН90ЁуЃЌ
ЁрOBЃН![]() ЃЌ
ЃЌ
ЁрOCЃН2![]() ЃЌ
ЃЌ
ЁрЕуBЕФзјБъЮЊ(Љ2![]() ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2
ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2![]() ЃЌ0)ЃЛ
ЃЌ0)ЃЛ
(2)жЄУїЃКзїAFЁЮECНЛxжсгкЕуFЃЌШчЭМвЛЫљЪОЃЌ
ЁпAEЁЮBCЃЌ
ЁрЫФБпаЮAFCEЪЧЦНааЫФБпаЮЃЌ
ЁрAEЃНFCЃЌAFЃНECЃЌ
ЁпAEЃНBDЃЌ
ЁрBDЃНCFЃЌ
гжЁпOBЃНOCЃЌ
ЁрODЃНOFЃЌ
дкЁїAODКЭЁїAOFжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїAODЁеЁїAOF(SAS)ЃЌ
ЁрADЃНAFЃЌ
ЁрADЃНECЃЌ
МДADЃНCEЃЛ
(3)ЕБЁїBP1GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМЖўЫљЪОЃЌ
ЁпMAЃНMP1ЃН4ЃЌЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌ
ЁрЕуP1ЕФзјБъЮЊ(Љ4ЃЌ2)ЃЛ
ЕБЁїBP2GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМЖўЫљЪОЃЌ
ЁпMAЃНMP2ЃН4ЃЌЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌ
ЁрЕуP2ЕФзјБъЮЊ(4ЃЌ2)ЃЛ
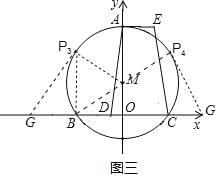
ЕБЁїBP3GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМШ§ЫљЪОЃЌ
ЁпOBЃН2![]() ЃЌOMЃН2ЃЌ
ЃЌOMЃН2ЃЌ
ЁрtanЁЯMBOЃН![]() ЃЌ
ЃЌ
ЁрЁЯMBOЃН30ЁуЃЌ
ЁрЁЯMBP3ЃН60ЁуЃЌ
ЁпBMЃНMP3ЃЌ
ЁрЁїBMP3ЪЧЕШБпШ§НЧаЮЃЌ
ЁрBP3ЃН4ЃЌ
ЁрЕуP3ЕФзјБъЮЊ(Љ2![]() ЃЌ4)ЃЛ
ЃЌ4)ЃЛ
ЕБЁїBP4GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМШ§ЫљЪОЃЌ
ЁпBP4ЃН8ЃЌЁЯP4BGЃН30ЁуЪБЃЌ
ЁрЕуP4ЕФзнзјБъЪЧЃК8ЁСsin30ЁуЃН8ЁС![]() ЃН4ЃЌКсзјБъЪЧЃКЉ2
ЃН4ЃЌКсзјБъЪЧЃКЉ2![]() +8ЁСcos30ЁуЃНЉ2
+8ЁСcos30ЁуЃНЉ2![]() +8ЁС
+8ЁС![]() ЃНЉ2
ЃНЉ2![]() +4
+4![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрЕуP4ЕФзјБъЮЊ(2![]() ЃЌ4)ЃЛ
ЃЌ4)ЃЛ
гЩЩЯПЩЕУЃЌШєЁїBPGЮЊжБНЧШ§НЧаЮЃЌЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2![]() ЃЌ4)ЃЌ(2
ЃЌ4)ЃЌ(2![]() ЃЌ4)ЃЎ
ЃЌ4)ЃЎ