Question

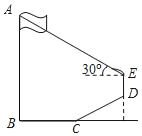
【题目】如图，点A在数轴上对应的数为20，以原点O为圆心，OA为半径作优弧，使点B在O右下方，且tan∠AOB＝，在优弧上任取一点P，且能过P作直线l∥OB交数轴于点Q，设Q在数轴上对应的数为x，连接OP．

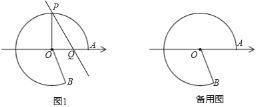
（1）若优弧上一段的长为10π，求∠AOP度数及x的值．

（2）若线段PQ的长为10，求这时x的值．

Answer 1

【答案】(1) ∠AOP=90°,x= ;(2) x的值为或﹣+5或．

【解析】

（1）由＝10π，解得n＝90°，即∠POQ＝90°，在Rt△POQ中，OP＝20，tan∠PQO＝tan∠QOB＝，即可得出x的值；

解：（1）如图1，

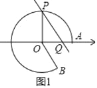
由＝10π，

解得n＝90°，

∴∠POQ＝90°，

∵PQ∥OB，

∴∠PQO＝∠BOQ，

∴tan∠PQO＝tan∠QOB＝＝

∴OQ＝

∴x＝；

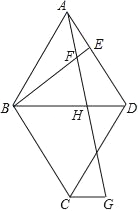
（2）分三种情况：

①如图2，作OH⊥PQ于H，设OH＝k，QH＝k．

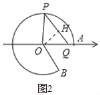
在Rt△OPH中，∵OP2＝OH2+PH2，

∴202＝（k）2+（10﹣k）2，

整理得：k2﹣5k﹣75＝0，

解得k＝或k＝（舍弃），

∴OQ＝2k＝

此时x的值为

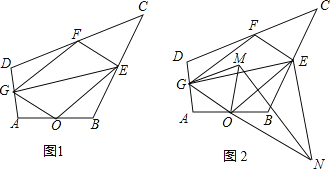
②如图3，作OH⊥PQ交PQ的延长线于H．设OH＝k，QH＝k．

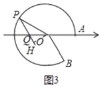
在Rt△在Rt△OPH中，∵OP2＝OH2+PH2，

∴202＝（k）2+（10+k）2，

整理得：k2+5k﹣75＝0，

解得k＝（舍弃）或k＝（舍弃），

∴OQ＝2k＝，

此时x的值为﹣+5

③如图4，作OH⊥PQ于H，设OH＝k，QH＝k．

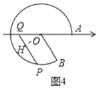
在Rt△OPH中，∵OP2＝OH2+PH2，

∴202＝（k）2+（10﹣k）2，

整理得：k2﹣5k﹣75＝0，

解得k＝或（舍弃），

∴OQ＝2k＝

此时x的值为．

综上所述，满足条件的x的值为或﹣+5或．