题目内容
11.如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )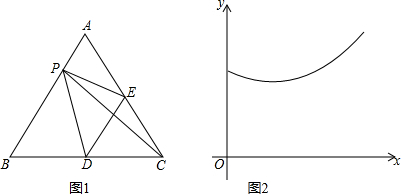
| A. | 线段DE | B. | 线段PD | C. | 线段PC | D. | 线段PE |
分析 先设等边三角形的边长为1个单位长度,再根据等边三角形的性质确定各线段取最小值时x的范围,最后结合函数图象得到结论.
解答  解:设等边三角形边长为1,则0≤x≤1,
解:设等边三角形边长为1,则0≤x≤1,
如图1,分别过点E、C、D作AB的垂线,垂足分别为F、G、H,
根据等边三角形的性质可知,
当x=$\frac{1}{4}$时,线段PE有最小值;
当x=$\frac{1}{2}$时,线段PC有最小值;
当x=$\frac{3}{4}$时,线段PD有最小值;
∵点E、D分别是AC,BC边的中点
∴线段DE的长为定值$\frac{1}{2}$.
根据图2可知,当x=$\frac{1}{4}$时,函数有最小值,故这条线段为PE.
故选(D)
点评 本题主要考查的是动点问题的函数图象,灵活运用等边三角形的性质和二次函数图象的对称性是解题的关键.解题时需要深刻理解动点的函数图象,了解图象中关键点所代表的实际意义.

练习册系列答案
相关题目
1.下列方程中,解是x=2的是( )
| A. | 3x+1=2x-1 | B. | 3x-1=2x+1 | C. | 3x+2x-2=0 | D. | 3x+2x+2=0 |
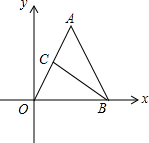 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点. 如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.
如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.