题目内容
如图,过原点的直线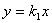 和
和 与反比例函数
与反比例函数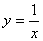 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时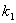 和
和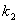 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(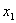 ,
,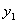 ),Q(
),Q( ,
,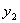 )(
)(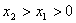 )是函数
)是函数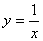 图象上的任意两点,
图象上的任意两点,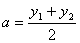 ,
,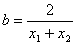 ,试判断
,试判断 ,
, 的大小关系,并说明理由.
的大小关系,并说明理由.

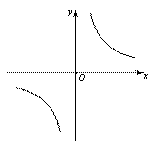
解:(1)∵直线y=k1x和y=k2x与反比例函数y= 的图象关于原点对称,
的图象关于原点对称,
∴OA=OC,OB=OD,
∴四边形ABCD 是平行四边形;
故答案为:平行;
(2)解:∵正比例函数y=k1x(k1>0)与反比例函数y= 的图象在第一象限相交于A,
的图象在第一象限相交于A,
∴k1x= ,解得x=
,解得x=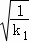 (因为交于第一象限,所以负根舍去,只保留正根)
(因为交于第一象限,所以负根舍去,只保留正根)
将x=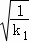 带入y=k1x得y=
带入y=k1x得y=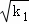 ,
,
故A点的坐标为(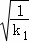 ,
,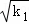 )同理则B点坐标为(
)同理则B点坐标为(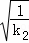 ,
,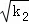 ),
),
又∵OA=OB,
∴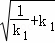 =
=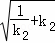 ,两边平分得得
,两边平分得得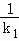 +k1=
+k1=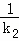 +k2,
+k2,
整理后得(k1﹣k2)(k1k2﹣1)=0,
∵k1≠k2,
所以k1k2﹣1=0,即k1k2=1;
(3)∵P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=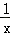 图象上的任意两点,
图象上的任意两点,
∴y1=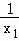 ,y2=
,y2=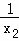 ,
,
∴a=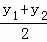 =
= =
=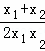 ,
,
∴a﹣b=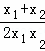 ﹣
﹣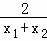 =
=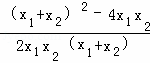 =
=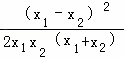 ,
,
∵x2>x1>0,
∴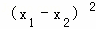 >0,x1x2>0,(x1+x2)>0,
>0,x1x2>0,(x1+x2)>0,
∴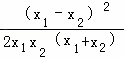 >0,
>0,
∴a﹣b>0,
∴a>b.

练习册系列答案
相关题目

 停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?
停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?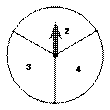
 对x恒成立,则n=_________.
对x恒成立,则n=_________. 分解因式,结果正确的是( )
分解因式,结果正确的是( ) B.
B.  C.
C.  D.
D. 
