题目内容
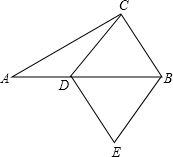 如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=________,平行四边形CDEB为菱形.
如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=________,平行四边形CDEB为菱形.

分析:首先根据勾股定理求得AB=5;然后利用菱形的对角线互相垂直平分、邻边相等推知OD=OB,CD=CB;最后Rt△BOC中,根据勾股定理得,OB的值,则AD=AB-2OB.
解答:
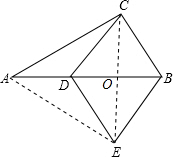 解:如图,连接CE交AB于点O.
解:如图,连接CE交AB于点O.∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=
 =5(勾股定理).
=5(勾股定理).若平行四边形CDEB为菱形时,CE⊥BD,且OD=OB,CD=CB.
∵
 AB•OC=
AB•OC= AC•BC,
AC•BC,∴OC=
 .
.∴在Rt△BOC中,根据勾股定理得,OB=
 =
=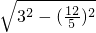 =
= ,
,∴AD=AB-2OB=
 .
.故答案是:
 .
.点评:本题考查了菱形的判定与性质.菱形的对角线互相垂直平分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
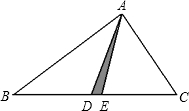 如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为
如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为 如图在Rt△ABC中,∠ACB=90°,sinA=
如图在Rt△ABC中,∠ACB=90°,sinA= 如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=
如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB= 如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是
如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=