题目内容
在平面直角坐标系中,已知点A(-
,0),B(
,0),点C在坐标轴上,且AC+BC=8,写出满足条件的所有点C的坐标 .
| 7 |
| 7 |
考点:两点间的距离公式
专题:分类讨论
分析:需要分类讨论:①当点C位于x轴上时,根据线段间的和差关系即可求得点C的坐标;②当点C位于y轴上时,根据勾股定理求点C的坐标.
解答:解:①当点C位于y轴上时,设C(0,b).
+
=8,解得,b=3或b=-3,
此时C(0,3),或C(0,-3).
②当点C位于x轴上时,设C(a,0).
则|-
-a|+|a-
|=8,即2a=8或-2a=8,
解得a=4或a=-4,
此时C(-4,0),或C(4,0).
综上所述,点C的坐标是:(0,3),(0,-3),(-4,0),(4,0).
故答案是:(0,3).(0,-3),(4,0),(-4,0).
(-
|
(
|
此时C(0,3),或C(0,-3).
②当点C位于x轴上时,设C(a,0).
则|-
| 7 |
| 7 |
解得a=4或a=-4,
此时C(-4,0),或C(4,0).
综上所述,点C的坐标是:(0,3),(0,-3),(-4,0),(4,0).
故答案是:(0,3).(0,-3),(4,0),(-4,0).
点评:本题考查了勾股定理、坐标与图形的性质.解题时,要分类讨论,以防漏解.另外,当点C在y轴上时,也可以根据两点间的距离公式来求点C的坐标.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )
如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )| A、0点 | B、1点 | C、2点 | D、3点 |
 如图a,b为数轴上的两点,下列结论正确的是( )
如图a,b为数轴上的两点,下列结论正确的是( )| A、b<-a<0<a<-b |
| B、a<-b<0<b<-a |
| C、a<b<0<-a<-b |
| D、-a<-b<0<b<a |
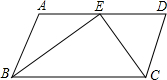 如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系.
如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系.