题目内容
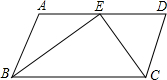 如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系.
如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系.考点:平行四边形的性质
专题:
分析:取BC的中点F,连接EF,要证明BE平分∠ABC,只需证明四边形ABFE为菱形,因为AE和BF既平行又相等,可先证平行四边形,又因为直角三角形斜边上的中线等于斜边的一半,可证EF=FB,即四边形ABFE为菱形,进而得出AE=ED=AB,即可得出答案.
解答: 解:取BC的中点F,连接EF.
解:取BC的中点F,连接EF.
∵E、F分别是AD、BC的中点,四边形ABCD为平行四边形,
∴AE∥BF,即四边形ABFE为平行四边形.
又∵∠BEC=90°,F为BC的中点,
∴EF=
BC=BF.
∴四边形ABFE为菱形,
∴AB=AE,
又∵AE=DE,
∴AD=2AB.
 解:取BC的中点F,连接EF.
解:取BC的中点F,连接EF.∵E、F分别是AD、BC的中点,四边形ABCD为平行四边形,
∴AE∥BF,即四边形ABFE为平行四边形.
又∵∠BEC=90°,F为BC的中点,
∴EF=
| 1 |
| 2 |
∴四边形ABFE为菱形,
∴AB=AE,
又∵AE=DE,
∴AD=2AB.
点评:此题主要考查了平行四边形的性质和菱形的判定,得出AE=AB是解题关键.

练习册系列答案
相关题目
 如图,?ABCD的对角线相交于点O,AB=8cm,两条对角线长的和为24cm,则△COD的周长为( )
如图,?ABCD的对角线相交于点O,AB=8cm,两条对角线长的和为24cm,则△COD的周长为( )| A、32cm | B、24cm |
| C、20cm | D、16cm |
绝对值小于5的非负数有( )
| A、9个 | B、4个 | C、5个 | D、2个 |
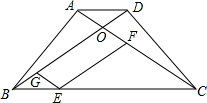 (1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
(1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.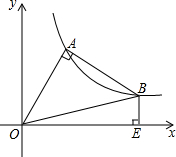 △OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=
△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y= 如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC=
如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC=