题目内容
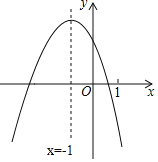
【题目】二次函数![]() 的图象如图,下列四个结论:
的图象如图,下列四个结论:
![]() ;
;
![]() ;
;
![]() 关于x的一元二次方程
关于x的一元二次方程![]() 没有实数根;
没有实数根;
![]() 为常数
为常数![]() .
.
其中正确结论的个数是![]()
![]()
A. 4个 B. 3个 C. 2个 D. 1个
【答案】D
【解析】分析:①根据对称轴列式,得b=2a,由图象可知:左交点的横坐标大于-3,当x=-3时,y<0,代入可得结论正确;
②开口向下,则顶点坐标的纵坐标是最大值,那么y=am2+bm+c<a-b+c,化简可得结论不正确;
③计算△的值作判断;
④比较k2与k2+1的值,根据当x>-1时,y随x的增大而减小,由图象得出结论.
详解:①因为二次函数的对称轴是直线x=-1,由图象可得左交点的横坐标大于-3,小于-2,
所以-![]() =-1,
=-1,
b=2a,
当x=-3时,y<0,
即9a-3b+c<0,
9a-6a+c<0,
3a+c<0,
∵a<0,
∴4a+c<0,
所以此选项结论正确;
②∵抛物线的对称轴是直线x=-1,
∴y=a-b+c的值最大,
即把x=m(m≠-1)代入得:y=am2+bm+c<a-b+c,
∴am2+bm<a-b,
m(am+b)+b<a,
所以此选项结论不正确;
③ax2+(b-1)x+c=0,
△=(b-1)2-4ac,
∵a<0,c>0,
∴ac<0,
∴-4ac>0,
∵(b-1)2≥0,
∴△>0,
∴关于x的一元二次方程ax2+(b-1)x+c=0有实数根;
④由图象得:当x>-1时,y随x的增大而减小,
∵当k为常数时,0≤k2≤k2+1,
∴当x=k2的值大于x=k2+1的函数值,
即ak4+bk2+c>a(k2+1)2+b(k2+1)+c,
ak4+bk2>a(k2+1)2+b(k2+1),
所以此选项结论不正确;
所以正确结论的个数是1个,
故选:D.

练习册系列答案
相关题目