题目内容
（1）
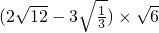
（2）tan260°+4sin30°cos45°-（π-5）0．
（1）解：原式=2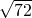
-3
=12-3
=9；
（2）解：原式=（
）2+4×
×
-1
=3+-1
=2+．
故答案为：9，2+．
分析：（1）根据二次根式混合运算的法则把括号内的每一项分别同
相乘，再把所得结果化为最简二次根式的形式，再合并同类项；
（2）分别根据特殊角的三角函数值及0指数幂的运算法则计算出各数，再根据实数混合运算的法则进行计算．
点评：本题考查的是二次根式的混合运算，特殊角的三角函数值及0指数幂的运算法则，熟知以上知识是解答此题的关键．
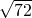-3=12
-3=9
；（2）解：原式=（
）2+4××-1=3+
-1=2+
．故答案为：9
，2+．分析：（1）根据二次根式混合运算的法则把括号内的每一项分别同
相乘，再把所得结果化为最简二次根式的形式，再合并同类项；（2）分别根据特殊角的三角函数值及0指数幂的运算法则计算出各数，再根据实数混合运算的法则进行计算．
点评：本题考查的是二次根式的混合运算，特殊角的三角函数值及0指数幂的运算法则，熟知以上知识是解答此题的关键．
练习册系列答案
相关题目
某校组织学生到涪江河某段测量两岸的距离，采用了两种方案收集数据．
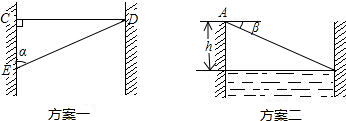
方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．
（1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一：
方案二：
（参考数据：tan1°24′=0.0244、tan2°16′=0.0396、tan1°56′=0.0338、tan76°33′=4.1814、tan71°35′=3.0032、tan65°25′=2.1859）
（2）由（1）表中数据计算：
方案一中河两岸平均宽为 米；
方案二中河两岸平均宽为 米；
（3）判断河两岸宽大约为 米；（从下面三个答案中选取，填入序号）
①390～420 ②420～450 ③350～480
（4）求出方案一的方差S12和方案二的方差S22，判断用哪种方案测量的误差较小．（精确到1）
方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．
（1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一：
| 测量次数 | 1 | 2 | 3 |
| EC（单位：米） | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 （单位：米） |
| 测量次数 | 1 | 2 | 3 |
| EC（单位：米） | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 （单位：米） |
（2）由（1）表中数据计算：
方案一中河两岸平均宽为
方案二中河两岸平均宽为
（3）判断河两岸宽大约为
①390～420 ②420～450 ③350～480
（4）求出方案一的方差S12和方案二的方差S22，判断用哪种方案测量的误差较小．（精确到1）
如图，AB为⊙O直径，CD为弦，AD与BC交于点E，∠CEA=α，则| S△CDE |
| S△ABE |
| A、cosα |
| B、sin2α |
| C、cos2α |
| D、tan2α |
如图，挂着“庆祝海门实验学校建校三周年”条幅的氢气球升在校园上空，已知气球的直径为4m，在地面A点测得气球中心O的仰角为∠OAD=60°，测得气球的视角∠BAC=2°（AB、AC为⊙O的切线，B、C为切点）．则气球中心O离地面的高度OD约为多少？