题目内容
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由D向C运动.沿直线AP翻折△ADP,形成如下四种情形.设DP=x,△ADP和矩形重叠部分(阴影)的面积为y.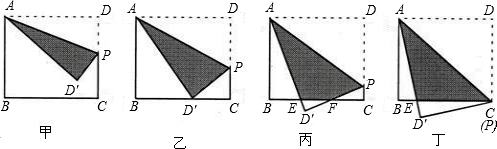
(1)如图丁,当点P运动到与C重合时,求重叠部分的面积y;
(2)如图乙,当点P运动到何处时,翻折△ADP后,点D恰好落在BC边上这时重叠部分的面积y等于多少?
(3)阅读材料:已知锐角α≠45°,tan2α是角2α的正切值,它可以用角α的正切值tanα来表示,即tan2α=
| 2tanα | 1-(tanα)2 |
(提示:在图丙中可设∠DAP=a)
分析:(1)根据三角形的面积公式,只需求得CE的长,根据平行线的性质以及折叠的性质发现等腰三角形ACE,设CE=m,则DE=10-m.在直角三角形CED′中,根据勾股定理即可求解;
(2)要求DP的长,也可在直角三角形CPD′中,根据勾股定理求解;
(3)根据(2)的结论,知分为两种情况讨论:当0≤x≤5时,由图甲知y=S△ADP;当5<x<8时,如图丙,重叠部分的面积即是直角梯形的面积减去两个直角三角形的面积.
(2)要求DP的长,也可在直角三角形CPD′中,根据勾股定理求解;
(3)根据(2)的结论,知分为两种情况讨论:当0≤x≤5时,由图甲知y=S△ADP;当5<x<8时,如图丙,重叠部分的面积即是直角梯形的面积减去两个直角三角形的面积.
解答:解:(1)由题意可得∠DAC=∠D′AC=∠ACE,∴AE=CE.
设AE=CE=m,则BE=10-m.
在Rt△ABE中,得m2=82+(10-m)2,∴m=8.2.
∴重叠部分的面积y=
•CE•AB=
×8.2×8=32.8(平方单位).
(另法:过E作EO⊥AC于O,由Rt△ABC∽Rt△EOC可求得EO).
(2)由题意可得△DAP≌△D′AP,
∴AD′=AD=10,PD′=DP=x.
在Rt△ABD′中,∵AB=8,∴BD′=
=6,于是CD′=4.
在Rt△PCD′中,由x2=42+(8-x)2,得x=5.
此时y=
•AD•DP=
×10×5=25(平方单位).
表明当DP=5时,点D恰好落在BC边上,这时y=25.
(另法:由Rt△ABD′∽Rt△PCD′可求得DP).
(3)由(2)知,DP=5是甲,丙两种情形的分界点.
当0≤x≤5时,由图甲知y=S△ADP=S△ADP=
•AD•DP=5x.
当5<x<8时,如图丙,设∠DAP=α,则∠AEB=2α,∠FPC=2α.
在Rt△ADP中,得tanα=
=
.
根据阅读材料,即tan2α=
,得出tan2α=
=
.
在Rt△ABE中,有BE=AB∕tan2α=
=
.
同理,在Rt△PCF中,有CF=(8-x)tan2α=
.
∴S△ABE=
•AB•BE=
×8×
=
.
S△PCF=
•PC•CF=
(8-x)×
=
.
而S梯形ABCP=
(PC+AB)×BC=
(8-x+8)×10=80-5x.
故重叠部分的面积y=S梯形ABCP-S△ABE-S△PCF=80-5x-
-
.
经验证,当x=8时,y=32.8适合上式.
综上所述,当0≤x≤5时,y=5x;当5<x≤8时,y=80-5x-
-
.
设AE=CE=m,则BE=10-m.
在Rt△ABE中,得m2=82+(10-m)2,∴m=8.2.
∴重叠部分的面积y=
| 1 |
| 2 |
| 1 |
| 2 |
(另法:过E作EO⊥AC于O,由Rt△ABC∽Rt△EOC可求得EO).
(2)由题意可得△DAP≌△D′AP,
∴AD′=AD=10,PD′=DP=x.
在Rt△ABD′中,∵AB=8,∴BD′=
| 102-82 |
在Rt△PCD′中,由x2=42+(8-x)2,得x=5.
此时y=
| 1 |
| 2 |
| 1 |
| 2 |
表明当DP=5时,点D恰好落在BC边上,这时y=25.
(另法:由Rt△ABD′∽Rt△PCD′可求得DP).
(3)由(2)知,DP=5是甲,丙两种情形的分界点.
当0≤x≤5时,由图甲知y=S△ADP=S△ADP=
| 1 |
| 2 |
当5<x<8时,如图丙,设∠DAP=α,则∠AEB=2α,∠FPC=2α.
在Rt△ADP中,得tanα=
| DP |
| AD |
| x |
| 10 |
根据阅读材料,即tan2α=
| 2tanα |
| 1-(tanα)2 |
2•
| ||
1-(
|
| 20x |
| 100-x2 |
在Rt△ABE中,有BE=AB∕tan2α=
| 8 | ||
|
| 2(100-x2) |
| 5x |
同理,在Rt△PCF中,有CF=(8-x)tan2α=
| 20x(8-x) |
| 100-x2 |
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2(100-x2) |
| 5x |
| 8(100-x2) |
| 5x |
S△PCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 20x(8-x) |
| 100-x2 |
| 10x(8-x)2 |
| 100-x2 |
而S梯形ABCP=
| 1 |
| 2 |
| 1 |
| 2 |
故重叠部分的面积y=S梯形ABCP-S△ABE-S△PCF=80-5x-
| 8(100-x2) |
| 5x |
| 10x(8-x)2 |
| 100-x2 |
经验证,当x=8时,y=32.8适合上式.
综上所述,当0≤x≤5时,y=5x;当5<x≤8时,y=80-5x-
| 8(100-x2) |
| 5x |
| 10x(8-x)2 |
| 100-x2 |
点评:此题要能够结合矩形的性质和折叠的性质发现对应的角相等和对应的线段相等,熟练运用勾股定理列方程求解.能够分情况讨论重叠部分的面积.难度较大.

练习册系列答案
相关题目
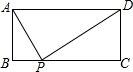 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
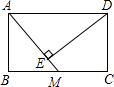 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.