题目内容
一司机驾驶汽车从甲地去乙地，以80千米∕小时的平均速度用6小时到达目的地．办完事情后，如果该司机必须在4.8小时内回到甲地，则返程时的平均速度不能低于（ ）
| A、80千米∕小时 |
| B、90千米∕小时 |
| C、100千米∕小时 |
| D、120千米∕小时 |
考点：一元一次不等式的应用
专题：
分析：首先根据题意，求解可得：S=V•t=480千米，汽车速度v（千米/小时）与时间t（小时）之间为反比例函数关系式，将数据代入用待定系数法可得反比例函数的关系式；由该解析式和t=4.8可进一步求解可得v的范围．
解答：解：甲地到乙地的距离S=80×6=480（千米）．
则v=
．
当t≤4.8时，v≥
=100（千米/小时）．
即返程时的平均速度不能低于100千米∕小时．
故选：C．
则v=
| 480 |
| t |
当t≤4.8时，v≥
| 480 |
| 4.8 |
即返程时的平均速度不能低于100千米∕小时．
故选：C．
点评：本题考查了一元一次不等式的应用，难度一般，关键是弄清楚速度、时间及距离三者的关系．
练习册系列答案
相关题目
下列每组数据分别表示三根木棒的长度，将它们首尾连接后，不能摆成三角形的一组是（ ）
| A、3，4，8 |
| B、5，8，11 |
| C、4，4，7 |
| D、8，8，15 |
下列命题是真命题的是（ ）
| A、方程3x2-4=2x的二次项系数为3，一次项系数为-2，常数项为-4 |
| B、同一时刻在阳光照射下，物体越长，地面上的影子越长 |
| C、四个角都是直角的两个四边形一定相似 |
| D、某种彩票中奖的概率是1%，买100张该种彩票一定会中奖 |
以下四个命题：
①在同一平面内，过一点有且只有一条直线与已知直线垂直；
②若a＞b，则-2a＞-2b；
③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行；
④对顶角相等．
其中真命题有（ ）个．
①在同一平面内，过一点有且只有一条直线与已知直线垂直；
②若a＞b，则-2a＞-2b；
③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行；
④对顶角相等．
其中真命题有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
已知x2-5x-1=0，则代数式2x2-5x+x-2的值是（ ）
| A、22 | B、24 | C、26 | D、28 |
（-3）100×（-3）-101等于（ ）
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
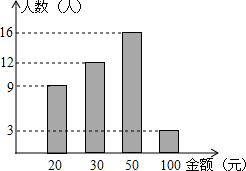春节将至，某中学八年级（1）班共有40名同学参加了“春节送温暖”捐款活动．活动结束后，生活委员小林将捐款情况进行了统计，并绘制成如右的统计图．