题目内容
1. 如图,反比例函数y=$\frac{-6}{x}$的图象经过点A,则S△ABO的值是( )
如图,反比例函数y=$\frac{-6}{x}$的图象经过点A,则S△ABO的值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据反比例函数的意义k=xy,根据三角形的面积等于$\frac{|xy|}{2}$,可得答案.
解答 解:由函数的意义,得
k=xy=-6,
S△ABO=$\frac{|xy|}{2}$=$\frac{|-6|}{2}$=3,
故选:B.
点评 本题考查了反比例函数k的几何意义,利用反比例函数的意义:xy=k,三角形的面积是S△ABO=$\frac{|xy|}{2}$=$\frac{|-k|}{2}$.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11.下列说法中正确的是( )
| A. | +(-3)的相反数是-3 | B. | -(+6)的相反数是-6 | ||
| C. | 整数的相反数一定是整数 | D. | 0没有相反数 |
12.把不等式-x≤2的解集在数轴上表示,正确的表示是( )
| A. |  | B. |  | C. |  | D. |  |
16.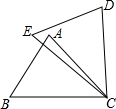 如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
 如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )| A. | BC=EC,∠B=∠E | B. | BC=EC,AC=DC | C. | ∠B=∠E,∠A=∠D | D. | BC=EC,∠A=∠D |
6.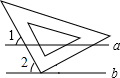 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
13.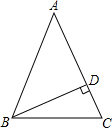 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )| A. | $\frac{1}{2}$∠A | B. | $\frac{1}{2}$∠B | C. | $\frac{1}{2}$(90°-∠B) | D. | $\frac{1}{2}$(90°-∠A) |
11.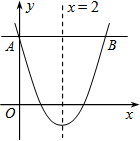 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (3,4) | D. | (4,3) |
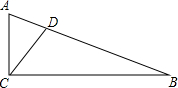 如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$.
如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$.