题目内容
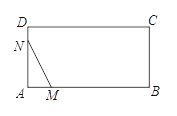
【题目】在![]() 中,
中,![]() ,
,![]() .点
.点![]() 是平面内不与点
是平面内不与点![]() ,
,![]() 重合的任意一点.连接
重合的任意一点.连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
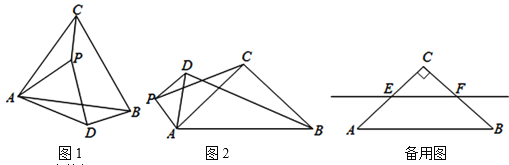
(1)观察猜想
如图1,当![]() 时,
时,![]() 的值是______,直线
的值是______,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是____________.(提示:求角度时可考虑延长
相交所成的较小角的度数是____________.(提示:求角度时可考虑延长![]() 交
交![]() 的延长线于
的延长线于![]() )
)
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的小角的度数,并就图2的情形说明理由.
相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当![]() 时,若点
时,若点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,请直接写出点
上,请直接写出点![]() ,
,![]() ,
,![]() 在同一直线上时
在同一直线上时![]() 的值_______________.
的值_______________.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,
,![]()
【解析】
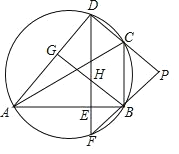
(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.证明△CAP≌△BAD(SAS),即可解决问题.
(2)如图2中,设BD交AC于点O,BD交PC于点E.证明△DAB∽△PAC,即可解决问题.
(3)分两种情形:①如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.利用直角三角形斜边上的中线的性质及等边对等角证得BH=BA,∠H=∠BAH,再根据四点共圆的知识求得∠DAC=∠DCA=22.5![]() ,证明AD=DC即可解决问题.
,证明AD=DC即可解决问题.
②如图3﹣2中,当点P在线段CD上时,根据三角形中位线的性质结合三线合一的性质证明DA=DC即可解决问题.
解:(1)如图1中,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,设
,设![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,
∵![]() ,,
,,
∴![]() ,
,
在![]() 和
和![]() 中,
中,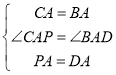 ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,线
,线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ,
,
故答案为![]() ,
,![]() .
.
图1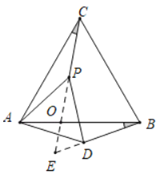
(2)如图2中,设![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
![]() ,
,
∵![]()
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 与直线
与直线![]() 相交所成的小角的度数为
相交所成的小角的度数为![]() .
.
图2
(3)![]() ,
,![]()
如图3﹣1中,当点![]() 在线段
在线段![]() 上时,延长
上时,延长![]() 交
交![]() 的延长线于
的延长线于![]() .
.
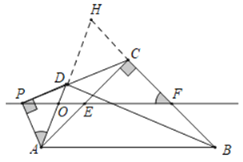
图3-1
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,
四点共圆,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
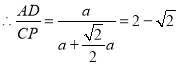 .
.
如图3﹣2中,当点![]() 在线段
在线段![]() 上时,设AB交CD于G,
上时,设AB交CD于G,
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,
上,
∴点![]() 为CG中点,
为CG中点,
∵AP⊥CG,
∴AC=AG, ∠ACD=∠AGC,
∵![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
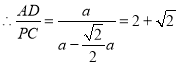 .
.
![]() 的值是
的值是![]() ,
,![]() .
.
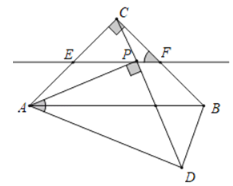
图3-2