题目内容
7．
如图，一个几何体的三视图分别是两个矩形、一个扇形，则这个几何体表面积的大小为12+15π．
分析 由几何体的三视图得出该几何体的表面是由3个长方形与两个扇形围成，结合图中数据求出组合体的表面积即可．
解答 解：由几何体的三视图可得：
该几何体的表面是由3个长方形与两个扇形围成，
该几何体的表面积为：S=2×2×3+$\frac{270π×{2}^{2}}{360}$×2+$\frac{270π×2}{180}$×3=12+15π，
故答案为：12+15π．
点评 本题考查了由几何体三视图求几何体的表面积的应用问题，考查了空间想象能力，由三视图复原成几何体是解决问题的关键．
练习册系列答案
相关题目
17．
已知一次函数y=kx+b（k≠0）的图象如图所示，则不等式kx+b＞1的解集为（ ）
已知一次函数y=kx+b（k≠0）的图象如图所示，则不等式kx+b＞1的解集为（ ）| A． | x＜0 | B． | x＞0 | C． | x＜2 | D． | x＞2 |
15．一元二次方程x2-2x=0根的判别式的值为（ ）
| A． | 4 | B． | 2 | C． | 0 | D． | -4 |
2．某车间有27名工人，生产某种由一个螺栓套两个螺母的产品，每人每天生产螺母16个或螺栓22个，若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套，则下面所列方程中正确的是（ ）
| A． | 22x=16（27-x） | B． | 16x=22（27-x） | C． | 2×16x=22（27-x） | D． | 2×22x=16（27-x） |
如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM=∠DAC．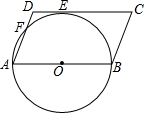
如图，在?ABCD中，AB为⊙O的直径，⊙O与DC相切于点E，与AD相交于点F，已知AB=12，∠C=60°，则$\widehat{FE}$的长为π．
16．在下列的计算中，正确的是（ ）
| A． | m3+m2=m5 | B． | m5÷m2=m3 | C． | （2m）3=6m3 | D． | （m+1）2=m2+1 |