题目内容
11.解不等式组.(1)$\left\{\begin{array}{l}{2-3(x-1)≤2x+15}\\{\frac{14}{3}-\frac{2-4x}{3}≥2x}\end{array}\right.$
(2)-2<1-0.2x<0.6.
分析 (1)分别解两个不等式得到x≥-2和x≤6,然后利用大小小大中间找确定不等式组的解集;
(2)把原不等式写成不等式组$\left\{\begin{array}{l}{-2<1-0.2x①}\\{1-0.2x<0.6②}\end{array}\right.$,然后解不等式组即可.
解答 (1)解:$\left\{\begin{array}{l}{2-3(x-1)≤2x+15①}\\{\frac{14}{3}-\frac{2-4x}{3}≥2x②}\end{array}\right.$
解不等式①,得x≥-2,
解不等式②,得x≤6
所以不等式组的解集是:-2≤x≤6;
(2)解:把原不等式写成不等式组$\left\{\begin{array}{l}{-2<1-0.2x①}\\{1-0.2x<0.6②}\end{array}\right.$
解不等式①,得x<15
解不等式②,得x>2
因此原不等式组的解集是:2<x<15.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
7.在以下一列数3,3,5,6,7,8中,中位数是( )
| A. | 3 | B. | 5 | C. | 5.5 | D. | 6 |
19.|-5+2|=( )
| A. | -7 | B. | 7 | C. | -3 | D. | 3 |
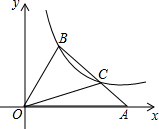 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴上的正半轴上,BC=2AC,点B、C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积为6.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴上的正半轴上,BC=2AC,点B、C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积为6.