题目内容

10．已知两圆半径分别为3和5，圆心距为2，则这两圆的位置关系是（　　）
A．内切B．外切C．相交D．相离

分析 由两圆的半径分别为3和5，圆心距为2，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．

解答 解：∵两圆的半径分别为3和5，圆心距为2，
又∵5-3=2，
∴两圆的位置关系是：内切．
故选A．

点评 本题主要考查了圆与圆的位置关系．解题的关键是掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系．

练习册系列答案
相关题目
20．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（　　）
A．正方形B．菱形C．矩形D．三角形
1．化简（a2-2+a-2）÷（a2-a-2）的结果为（　　）
A．1B．-1C．$\frac{{a}^{2}-1}{{a}^{2}+1}$D．$\frac{{a}^{2}+1}{{a}^{2}-1}$
18．如图在3×4的网格中，每个小正方形的边长都是1个单位长度，定义：以网格中小正方形的顶点为顶点的正方形叫作格点正方形，图中包含“△”的格点正方形的个数有（　　）
A．5个B．6个C．7个D．8个
5．如图（1）所示，E为矩形ABCD的边AD上一边，动点P，Q同时从点B出发，点P沿折线BE-ED-DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒，设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分）则下列结论正确的是（　　）
A．AB：AD=3：4
B．当△BPQ是等边三角形时，t=5秒
C．当△ABE∽△QBP时，t=7秒
D．当△BPQ的面积为4cm2时，t的值是$\sqrt{10}$或$\frac{47}{5}$秒
15．要使分式$\frac{1}{2-x}$有意义，则x的取值范围是（　　）
A．x＞2B．x＜2C．x≠-2D．x≠2
2．下列计算中正确的是（　　）
A．x4•x4=x16B．（a3）2=a5C．a6÷a3=a2D．a+2a=3a
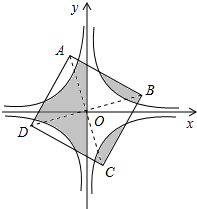19．在平面直角坐标系中，有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD，原点O与对角线AC，BD的交点重合，且如图所示的阴影部分面积为8，则AB的长是（　　）
A．2B．4C．6D．8
16．阅读下列材料并解答问题：
我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离，即|x|=|x-0|．也就是说，|x|表示在数轴上数x与数0对应的点之间的距离．
        这个结论可以推广为|x1-x2|表示在数轴上数x1与x2对应的点之间的距离．
例1：解方程|x|=2，容易看出，在数轴上与原点距离为2点的对应数为±2，即该方程的解为x=±2
例2：解不等式|x-1|＞2，如图1，在数轴上找出|x-1|=2的解，即到1的距离为2的点对应的数为-1，3，则|x-1|＞2的解集为x＜-1或x＞3．
例3：解方程|x-1|+|x+2|=5．由绝对值的几何意义知，该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值．在数轴上，1和-2的距离为3，满足方程的x对应的点在1的右边或-2的左边，若x对应点在1的右边，由图2可以看出x=2．同理，若x对应点在-2的左边，可得x=-3，故原方程的解是x=2或x=-3．

问答问題：（只需直接写出答案）
①解方程丨x+3|=4
②解不等式|x-3|≥4
③解方程|x-3|+|x+2|=8．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网