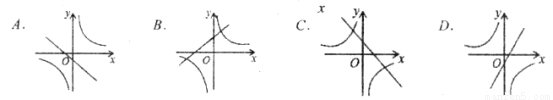题目内容
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是
的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是 ;求:
;求:

(1)一次函数的解析式;
(2)根据图像回答,当一次函数的值大于反比例函数的值时,写出x的取值范围;
(3)求 △AOB的面积。
(1) y=-x+2;(2) x<-2或0<x<4;(3)6.
【解析】
试题分析:(1)先求出点A、B的坐标,然后利用待定系数法求一次函数解析式解答;
(2)根据图象回答即可.
(3)先求出一次函数与x轴的交点M的坐标,从而得到OM的长度,然后根据△AOB的面积等于△AOMC与△BOM的面积的和列式计算即可得解.
试题解析:(1)当x=-2时,y=- =4,
=4,
当y=-2时,- =-2,解得x=4,
=-2,解得x=4,
所以点A、B的坐标为A(-2,4),B(4,-2),
∵反比例函数图象与一次函数y=kx+b的图象交于A、B两点,
∴ ,解得
,解得 ,
,
∴一次函数的解析式为y=-x+2;
(2)根据图象得:
当x<-2或0<x<4时,一次函数的值大于反比例函数的值.
(3)当y=0时,-x+2=0,
解得x=2,
所以点M的坐标为(2,0),
所以OM=2,
S△AOB=S△AOM+S△BOM= ×2×4+
×2×4+ ×2×2=4+2=6.
×2×2=4+2=6.
考点:反比例函数与一次函数的交点问题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目

 cm.用代数式表示阴影部分面积S.
cm.用代数式表示阴影部分面积S.  有实数解,则m的取值范围是( )
有实数解,则m的取值范围是( )
 .
. 是锐角,且
是锐角,且 计算
计算
 的山坡上种树,要求株距(相邻两树间的水平距离)是
的山坡上种树,要求株距(相邻两树间的水平距离)是 米,斜坡上相邻两树间的坡面距离是 米.
米,斜坡上相邻两树间的坡面距离是 米.

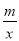 (m≠0)的图象可能是( )
(m≠0)的图象可能是( )