题目内容
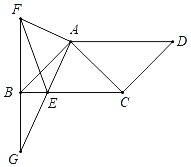
【题目】现有一块直角三角形的铁皮
，
，
，
．要在其中剪出一个面积尽可能大的正方形，小红和小亮各想出了甲、乙两种方案，请你帮忙算一算哪一种方案剪出的正方形面积较大？
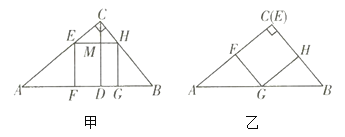
【答案】方案乙剪出的正方形面积较大．
【解析】
对于方案甲：先利用勾股定理计算出AB＝100，再利用面积法计算出CD＝48，设正方形EFGH的边长为x，证明△CEH∽△CAB，然后列出比利式可计算出
；对于方案乙：设正方形EFGH的边长为y，证明
∽
，列出比利式可计算出
，然后比较x和y的大小即可判断哪一种方案剪出的正方形面积较大．
解：方案甲：设正方形的边长为
，
在中，
，
，
，
∴
，
∵
于点
，
∴
，
∵
，
∴
∽
，
∵
，，
∴
，
∴
，
解得；
方案乙：设正方形的边长为
，
∵
，
∴∽，
∴
，即
，
解得，
∵
，
∴方案乙剪出的正方形面积较大．
练习册系列答案
相关题目
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：
，每件产品的利润z（元）与月份x（月）的关系如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
