Question

【题目】如图，四边形ABCD是平行四边形，∠D＝45°，∠BAC＝90°，点E为BC边上一点，将AE绕点A按顺时针方向旋转90°后能与AF重合，且FB⊥BC，点G是FB与AE的交点，点E是AG的中点．

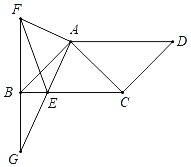
（1）若AG＝2，BE＝1，求BF的长；

（2）求证：AB＝BG+2BE．

Answer 1

【答案】（1）BF＝3；（2）见解析.

【解析】

（1）求出AE=GE=AG=，由旋转的性质得出∠GAF=90°，AF=AE=，由勾股定理得出GF==5，BG==2．即可得出答案；
（2）作延长DA交BF于M，作AN⊥BC于N，证出△ABC是等腰直角三角形，得出AB=AC，BC=AB，得出AN=BC=BN=CN，证出四边形AMBN是正方形，即可有AM=BM=BN=AN=CN，证出BE是△AMG的中位线，得出BM=BG，AM=2BE，因此BN=BM=BG=AM=2BE，BE=NE，即可得出结论．

（1）解：∵点E是AG的中点，

∴AE＝GE＝AG＝，

由旋转的性质得：∠GAF＝90°，AF＝AE＝，

∴GF＝＝＝5，

∵FB⊥BC，

∴∠EBG＝90°，

∴BG＝＝＝2．

∴BF＝GF﹣BG＝5﹣2＝3；

（2）证明：作延长DA交BF于M，作AN⊥BC于N，如图所示：

则∠AMB＝∠ANB＝∠ANC＝90°，

∵FB⊥BC，

∴四边形AMBN是矩形，

∵四边形ABCD是平行四边形，

∴∠ABC＝∠D＝45°，AD∥BC，

∵∠BAC＝90°，

∴△ABC是等腰直角三角形，

∴AB＝AC，BC＝AB，

∵AN⊥BC，

∴AN＝BC＝BN＝CN，

∴四边形AMBN是正方形，

∴AM＝BM＝BN＝AN＝CN，

∵点E是AG的中点，MD∥BC，

∴BE是△AMG的中位线，

∴BM＝BG，AM＝2BE，

∴BN＝BM＝BG＝AM＝2BE，

∴BE＝NE，

∵BC＝CN+EN+BE＝BG+2BE，

∴AB＝BG+2BE．