��Ŀ����
����Ŀ��ǭ������ij���й����ס���������Ʒ����֪����3������Ʒ��2������Ʒ����60Ԫ������2������Ʒ��3������Ʒ����65Ԫ��
��1���ס���������Ʒ�Ľ������۷ֱ��Ƕ��٣�
��2�������Ʒ�����۵���Ϊx����λ��Ԫ/�����������۹����з��֣���11��x��19ʱ������Ʒ����������y����λ�����������۵���x֮�����һ�κ�����ϵ��x��y֮��IJ�����ֵ��Ӧ��ϵ�����
���۵���x��Ԫ/���� | 11 | 19 |
��������y������ | 18 | 2 |
��д����11��x��19ʱ��y��x֮��ĺ�����ϵʽ��
��3���ڣ�2���������£������Ʒ������������ΪwԪ��������Ʒ�����۵���x��Ԫ/������Ϊ����ʱ�����������������������Ƕ��٣�
���𰸡���1���ס���������Ʒ�Ľ������۷ֱ���10��15Ԫ/������2��y����2x+40��11��x��19������3��������Ʒ�����۵��۶�Ϊ15Ԫ/��ʱ������������������������50Ԫ��
��������
��1����ס���������Ʒ�Ľ������۷ֱ���a��bԪ/����Ȼ���г���Ԫһ�η����鲢��⼴�ɣ�
��2����y��x֮��ĺ�����ϵʽΪy��k1x+b1���ô���ϵ������⼴�ɣ�
��3�����г�������������ĺ�����ϵʽ��Ȼ�����ö��κ�������������ֵ���ɣ�
�⣺��1����ס���������Ʒ�Ľ������۷ֱ���a��bԪ/����������ã�
![]() ��
��
��ã�![]() ��
��
��ס���������Ʒ�Ľ������۷ֱ���10��15Ԫ/����
��2����y��x֮��ĺ�����ϵʽΪy��k1x+b1������11��18������19��2������ã�
 ����ã�
����ã� ��
��
��y��x֮��ĺ�����ϵʽΪy����2x+40��11��x��19����
��3��������ã�
w������2x+40����x��10��
����2x2+60x��400
����2��x��15��2+50��11��x��19����
�൱x��15ʱ��wȡ�����ֵ50��
�൱����Ʒ�����۵��۶�Ϊ15Ԫ/��ʱ������������������������50Ԫ��

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�����Ŀ��ijУΪ���ѧ���忼�ɼ�����ȫУ300�����꼶ѧ������һ��������ѵ����Ϊ�˽�ѧ��ѵ��Ч����ѧУ�������ھ��꼶��ѧ�ڿ�ѧ����ѧ��ĩ�ֱ�Ծ��꼶ѧ������һ�����������ԣ�ѧ���ɼ���Ϊ����������20�֣�����18��Ϊ���㣮�������ȡ��ͬһ����ѧ�������γɼ����������������ͷ��������ɼ��÷���x��ʾ�����ֳ����飺A��x��13��B.13��x��15��C.15��x��17��D.17��x��19��E.19��x��20��
��ѧ����ȡѧ���ijɼ���D���е������ǣ�17��17��17��17��17��18��18��
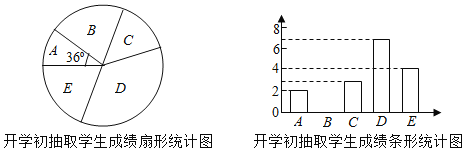
ѧ��ĩ��ȡѧ���ɼ�ͳ�Ʊ�
ѧ���ɼ� | A�� | B�� | C�� | D�� | E�� |
���� | 0 | 1 | 4 | 5 | a |
�������ݣ�
ƽ���� | ��λ�� | ���� | |
��ѧ����ȡѧ���ɼ� | 16 | b | 17 |
ѧ��ĩ��ȡѧ���ɼ� | 18 | 18.5 | 19 |
����������Ϣ������������⣺
��1��ֱ��д��ͼ����a��b��ֵ������ȫ����ͳ��ͼ��
��2�������У���꼶ѧ�����μ������β��ԣ����Ƹ�Уѧ��ĩ�ɼ������ѧ�������ȿ�ѧ���ɼ������ѧ�����������˶��٣�
��3��С��ѧ�����Գɼ�16�֣�ѧ��ĩ���Գɼ�19�֣����ݳ���������ݣ���ѡ��һ�����ʵ�ͳ��������С���ѵ��Ч����