题目内容
已知关于x的一元二次方程x2-(2k-1)x+k2+1=0有实数根x1,x2,且x12+x22=17,求k的值.
考点:根与系数的关系,根的判别式
专题:计算题
分析:先根据根的判别式确定k的取值范围,再根据根与系数的关系得x1+x2=2k-1,x1x2=k2+1,接着利用完全平方公式得到x12+x22=(x1+x2)2-2x1x2,则(2k-1)2-2(k2+1)=17,然后解关于k的一元二次方程,最后根据k的范围确定k的值.
解答:解:根据题意得△=(2k-1)2-4(k2+1)≥0,解得k≤-
,
∵x1+x2=2k-1,x1x2=k2+1,
而x12+x22=(x1+x2)2-2x1x2,
∴(2k-1)2-2(k2+1)=17,
整理得k2-2k-9=0,解得k1=1+
,k2=1-
,
而k≤-
,
∴k=1-
.
| 3 |
| 4 |
∵x1+x2=2k-1,x1x2=k2+1,
而x12+x22=(x1+x2)2-2x1x2,
∴(2k-1)2-2(k2+1)=17,
整理得k2-2k-9=0,解得k1=1+
| 10 |
| 10 |
而k≤-
| 3 |
| 4 |
∴k=1-
| 10 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
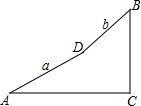 如图:BC⊥AC,设AD=a,DB=b,∠A=α,∠B=β,则用含a、b、α、β的式子表示AC正确的为( )
如图:BC⊥AC,设AD=a,DB=b,∠A=α,∠B=β,则用含a、b、α、β的式子表示AC正确的为( )| A、asinα+bsinβ |
| B、asinα+bcosβ |
| C、acosα+bsinβ |
| D、acosα+bcosβ |
 如图所示,AB、CD是⊙O的两条直径,OE⊥AB,OF⊥CD,则
如图所示,AB、CD是⊙O的两条直径,OE⊥AB,OF⊥CD,则