题目内容
11.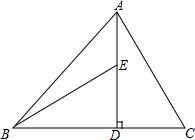 如图,在△ABC中,AD⊥BC于D,点E在AD上且AC=BE,DE=CD,求∠BAD的度数.
如图,在△ABC中,AD⊥BC于D,点E在AD上且AC=BE,DE=CD,求∠BAD的度数.
分析 由题意得出△BDE和△ADC是直角三角形,由HL证明Rt△BDE≌Rt△ADC,得出BD=AD,△ABD是等腰直角三角形,即可得出结果.
解答 解:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
∴△BDE和△ADC是直角三角形,
在Rt△BDE和Rt△ADC中,$\left\{\begin{array}{l}{BE=AC}\\{DE=CD}\end{array}\right.$,
∴Rt△BDE≌Rt△ADC(HL),
∴BD=AD,
∴△ABD是等腰直角三角形,
∴∠BAD=45°.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握直角三角形全等的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2. 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )
已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )
 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )
已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )| A. | abc<0 | B. | a+b+c>0 | C. | a-2b+4c<0 | D. | b+2c>0 |
 如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=65°,则∠2=115°.
如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=65°,则∠2=115°.


 如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米.
如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米.