Question

12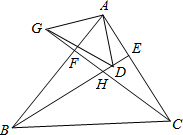．如图，在△ABC中，BE，CF分别是AC，AB边上的高，在BE上截取BD=AC，延长CF至G，使CG=AB，连接AD，AG，GD，试判断△AGD的形状．

Answer 1

分析 由BE垂直于AC，CF垂直于AB，利用垂直的定义得到一对角相等，再由一对对顶角相等，利用两对对应角相等的两三角形相似得到三角形BHF与三角形CHE相似，由相似三角形的对应角相等得到一对角相等，再由AB=CG，BD=AC，利用SAS可得出三角形ABD与三角形ACG全等，由全等三角形的对应边相等可得出AD=AG．

解答 解：△AGD是等腰直角三角形，
理由：∵BE⊥AC，CF⊥AB，
∴∠HFB=∠HEC=90°，又∵∠BHF=∠CHE，
∴∠ABD=∠ACG，
在△ABD和△GCA中
$\left\{\begin{array}{l}{AB=CG}\\{∠ABD=∠ACG}\\{BD=CA}\end{array}\right.$，
∴△ABD≌△GCA（SAS），
∴AD=GA，∠AGC=∠BAD，
∵CF⊥AB，
∴∠GAF+∠AGF=90°，
∴∠GAF+∠BAD=90°，∴∠GAD=90°
∴△AGD是等腰直角三角形．

点评 此题考查了全等三角形的判定与性质，等腰三角形的判定，熟练掌握判定与性质是解本题的关键．