题目内容
如图,△ABC内有一点K,过K引三边的平行线与三边交成的线段,有同一长度x ,如果BC、AC、AB长度分别为a、b、c,试求x.
,如果BC、AC、AB长度分别为a、b、c,试求x.
分析:在△ABC中有三个平行四边形,把它们的边分别表示出来,同时还有三个三角形与△ABC相似,根据对应线段的比相等进行计算可以求出x的值.
解答:解:如图:
在△ABC内有三个平行四边形,分别把它们的边用d,e,f,g,m,n表示.
同时在△ABC中有三个三角形与△ABC相似,则有:
=
=
,
=
=
,
=
=
.
∴
+
+
=
+
+
=
+
+
.
∴
+
+
=
(
+
+
),
=
(1-
+1-
+1-
),
整理得:
+
+
=1,
=
+
+
=
,
∴x=
.
在△ABC内有三个平行四边形,分别把它们的边用d,e,f,g,m,n表示.
同时在△ABC中有三个三角形与△ABC相似,则有:
| x |
| a |
| g |
| b |
| n |
| c |

| x |
| b |
| m |
| c |
| f |
| a |
| x |
| c |
| e |
| a |
| d |
| b |
∴
| x |
| a |
| x |
| b |
| x |
| c |
| g |
| b |
| m |
| c |
| e |
| a |
| n |
| c |
| f |
| a |
| d |
| b |
∴
| x |
| a |
| x |
| b |
| x |
| c |
| 1 |
| 2 |
| e+f |
| a |
| d+g |
| b |
| m+n |
| c |
=
| 1 |
| 2 |
| x |
| a |
| x |
| b |
| x |
| c |
整理得:
| x |
| a |
| x |
| b |
| x |
| c |
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| bc+ac+ab |
| abc |
∴x=
| abc |
| ab+bc+ac |
点评:本题考查的是相似三角形的判定与性质,根据平行线可以判定图中有三个三角形与原来的三角形相似,另外还有三个是平行四边形,根据相似三角形和平行四边形的性质进行计算求出X的值.

练习册系列答案
相关题目
 在格点上,其中A点坐标为(-2,3).请你解答下列问题:
在格点上,其中A点坐标为(-2,3).请你解答下列问题:
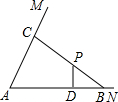 如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.
如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.
 如图,在△ABC内有一矩形,D在AB边上,G在AC边上,EF在斜边BC上,已知AB=3,AC=4,矩形DEFG的面积等于
如图,在△ABC内有一矩形,D在AB边上,G在AC边上,EF在斜边BC上,已知AB=3,AC=4,矩形DEFG的面积等于 ,则BE的长等于________.
,则BE的长等于________.