题目内容
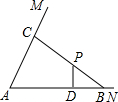 如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.
如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.
分析:可证明,当过点P的直线满足PB=PC时,△ABC的面积最小.设B1C1为过点P的任一直线,构成△AB1C1.作CF∥B1B,可证明△PCF≌△PBB1,则S△ABC=S△PCF+S四边形AB1PC<S△AB1C1.即可求出CE,再由tan∠MAN=3,可得AE,从而得出BD,即可得出△ABC面积的最小值.
解答: 解:可证明,当过点P的直线满足PB=PC时,△ABC的面积最小.
解:可证明,当过点P的直线满足PB=PC时,△ABC的面积最小.
事实上,设B1C1为过点P的任一直线,构成△AB1C1.
如图,作CF∥B1B,则△PCF≌△PBB1,
故S△ABC=S△PCF+S四边形AB1PC<S△AB1C1.
根据上述的几何结论计算如下.
因为PD=12,所以CE=24,
又因为tan∠MAN=3,
所以AE=8,
由ED=BD,
而ED=AD-AE=22,
得BD=22.
故AB=AD+BD=52.
(S△ABC)min=
AB•CE=624.
 解:可证明,当过点P的直线满足PB=PC时,△ABC的面积最小.
解:可证明,当过点P的直线满足PB=PC时,△ABC的面积最小.事实上,设B1C1为过点P的任一直线,构成△AB1C1.
如图,作CF∥B1B,则△PCF≌△PBB1,
故S△ABC=S△PCF+S四边形AB1PC<S△AB1C1.
根据上述的几何结论计算如下.
因为PD=12,所以CE=24,
又因为tan∠MAN=3,
所以AE=8,
由ED=BD,
而ED=AD-AE=22,
得BD=22.
故AB=AD+BD=52.
(S△ABC)min=
| 1 |
| 2 |
点评:本题是一道综合性的题目,考查了相似三角形的判定和性质、全等三角形的判定和性质以及解直角三角形,综合性较强,难度偏大.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
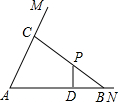 如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.
如图,在∠MAN内有一定点P,已知tan∠MAN=3,P到直线AN的距离PD=12,AD=30.过P任作一条直线分别与AN、AM交于点B、C.求△ABC面积的最小值.