题目内容
13.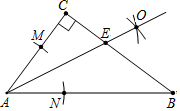 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径作弧,分别交AC、AB于点M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径作弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为6.
如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径作弧,分别交AC、AB于点M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径作弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为6.
分析 直接利用基本作图方法得出AE是∠CAB的平分线,进而结合全等三角形的判定与性质得出AC=AD,再利用勾股定理得出AC的长.
解答 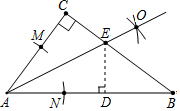 解:过点E作ED⊥AB于点D,
解:过点E作ED⊥AB于点D,
由作图方法可得出AE是∠CAB的平分线,
∵EC⊥AC,ED⊥AB,
∴EC=ED=3,
在Rt△ACE和Rt△ADE中,
$\left\{\begin{array}{l}{AE=AE}\\{EC=ED}\end{array}\right.$,
∴Rt△ACE≌Rt△ADE(HL),
∴AC=AD,
∵在Rt△EDB中,DE=3,BE=5,
∴BD=4,
设AC=x,则AB=4+x,
故在Rt△ACB中,
AC2+BC2=AB2,
即x2+82=(x+4)2,
解得:x=6,
即AC的长为:6.
故答案为:6.
点评 此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确得出BD的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.对如图的变化顺序描述正确的是( )


| A. | 翻折、旋转、平移 | B. | 旋转、翻折、平移 | C. | 平移、翻折、旋转 | D. | 翻折、平移、旋转 |
8. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
5.下列说法中错误的是( )
| A. | 近似数1.7与1.70表示的意义不同 | B. | 近似数0.03080有4个有效数字 | ||
| C. | 49553精确到万位是4.9×104 | D. | 5.230×104是精确到十位的近似数 |