题目内容
19.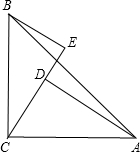 如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足为E,AD⊥CE,垂足为D.
如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足为E,AD⊥CE,垂足为D.(1)判断直线BE与AD的位置关系为互相平行,BE与AD之间的距离是线段DE的长;
(2)若AD=8cm,BE=6cm,求BE与AD之间的距离及AC的长.
分析 (1)根据“BE⊥CE,垂足为E,AD⊥CE,垂足为D”可以得出BE∥AD,进而得到线段DE的长是BE与AD之间的距离;
(2)根据题意,首先可以得出∠BCE=∠CAD,进而可以证明△BCE≌△CAD,据此即可得出DC、DE的长,再根据勾股定理得出AC的长.
解答 解:(1)∵BE⊥CE,∴∠BEC=90°,
∵AD⊥CE,∴∠ADC=90°,
∴∠BEC=∠ADC,
∴AD∥BE,
∴BE与AD之间的距离是线段DE的长;
(2)∵AD⊥CE,垂足为DBE⊥CE,垂足为E,∴∠ADC=∠CEB=90°,
∴∠DCA+∠CAD=90°,
又∵∠DCA+∠BCE=∠ACB=90°,
∴∠BCE=∠CAD,
在△CAD和△BCE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠CAD=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△CAD≌△BCE(AAS),
∴CE=AD=8cm,DC=BE=6cm,
∴DE=EC-DC=8-6=2(cm),
即:BE与AD之间的距离是2cm,
在Rt△ADC中,∠ADC=90°,
AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm).
点评 本题主要考查了两条直线平行的判定定理,两条平行线之间的距离,还考查了三角形全等的判定定理与性质定理,是经常考查的题目,要注意认真总结.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
10. E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
 E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )
E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为( )| A. | 25 | B. | 12 | C. | 13 | D. | 19 |
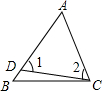 如图,已知∠1=∠2,∠B=60°,∠ACB=80°,则∠BCD的度数为10°.
如图,已知∠1=∠2,∠B=60°,∠ACB=80°,则∠BCD的度数为10°.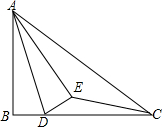 如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是边BC上的任意一点,以AD为折痕翻折△ABD,使点B落在点E处,连接EC,当△DEC为直角三角形时,BD的长为3或6.
如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是边BC上的任意一点,以AD为折痕翻折△ABD,使点B落在点E处,连接EC,当△DEC为直角三角形时,BD的长为3或6.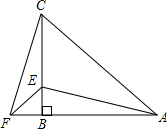 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.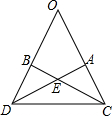 如图,OA=OB,AC=BD,AD、BC相交于点E,若∠O=50°,∠ODA=35°,则∠OCB=35°,∠CED=120°.
如图,OA=OB,AC=BD,AD、BC相交于点E,若∠O=50°,∠ODA=35°,则∠OCB=35°,∠CED=120°.