ЬтФПФкШн
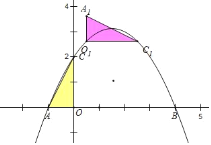
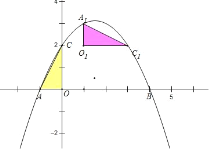
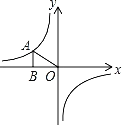
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпlНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљБэЪОЕФЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁЯACB=90ЁуЃЛ
ЃЈ3ЃЉдкЕуPдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЕУЁїBQMЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉСЌНгACЃЌНЋЁїAOCШЦЦНУцФкФГЕуHЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЁїA1O1C1ЃЌЕуAЁЂOЁЂCЕФЖдгІЕуЗжБ№ЪЧЕуA1ЁЂO1ЁЂC1ЁЂШєЁїA1O1C1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌФЧУДЮвУЧОЭГЦетбљЕФЕуЮЊЁАКЭаГЕуЁБЃЌЧыжБНгаДГіЁАКЭаГЕуЁБЕФИіЪ§КЭЕуA1ЕФКсзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() +x+2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛЃЈ4ЃЉСНИіКЭаГЕуЃЛ A1ЕФКсзјБъЪЧ1ЃЛ
+x+2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛЃЈ4ЃЉСНИіКЭаГЕуЃЛ A1ЕФКсзјБъЪЧ1ЃЛ![]() .
.
ЁОНтЮіЁП
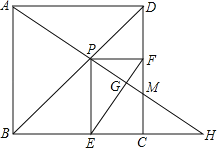
ЃЈ1ЃЉАбЕуAЃЈ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉШ§ЕуЕФзјБъДњШыКЏЪ§НтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃЛ
ЃЈ2ЃЉЯШЧѓГіABЁЂACЁЂBCЕФГЄЖШЃЌИљОнЙДЙЩЖЈРэМДПЩжЄУї;
ЃЈ3ЃЉЗжСНжжЧщПіЗжБ№ЬжТлЃЌЕБЁЯQBMЃН90ЁуЛђЁЯMQBЃН90ЁуЃЌМДПЩЧѓЕУQЕуЕФзјБъЃЎ
ЃЈ4ЃЉСНИіКЭаГЕуЃЛAOЃН1ЃЌOCЃН2ЃЌЩшA1ЃЈxЃЌyЃЉЃЌдђC1ЃЈx+2ЃЌyЉ1ЃЉЃЌO1ЃЈxЃЌyЉ1ЃЉЃЌЕБA1ЁЂC1дкХзЮяЯпЩЯЪБКЭO1ЁЂC1дкХзЮяЯпЩЯЪБЃЌЗжСНжжЧщПіСаЗНГЬзщПЩЕУA1ЕФКсзјБъ.
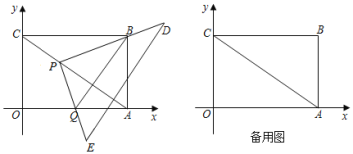
ЃЈ1ЃЉЩшХзЮяЯпНтЮіЪНЮЊyЃНax2+bx+cЃЌ
НЋЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉДњШыНтЮіЪНЃЌ
Ёр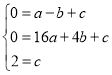 ЃЌЁр
ЃЌЁр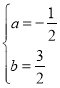 ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжЄУїЃКЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ Ёр
ЃЌ Ёр![]() ЃЌМДЁЯACB=90ЁуЃЛ
ЃЌМДЁЯACB=90ЁуЃЛ
ЃЈ3ЃЉЁпЕуCгыЕуDЙигкxжсЖдГЦЃЌЁрDЃЈ0ЃЌЉ2ЃЉЃЎ
ЩшжБЯпBDЕФНтЮіЪНЮЊyЃНkxЉ2ЃЎ
ЁпНЋЃЈ4ЃЌ0ЃЉДњШыЕУЃК4kЉ2ЃН0ЃЌ
ЁрkЃН![]() ЃЎЁржБЯпBDЕФНтЮіЪНЮЊyЃН
ЃЎЁржБЯпBDЕФНтЮіЪНЮЊyЃН![]() xЉ2ЃЎ
xЉ2ЃЎ
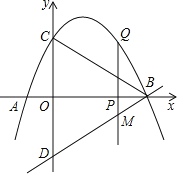
ЕБPЕугыAЕужиКЯЪБЃЌЁїBQMЪЧжБНЧШ§НЧаЮЃЌДЫЪБQЃЈЉ1ЃЌ0ЃЉЃЛ
ЕБBQЁЭBDЪБЃЌЁїBQMЪЧжБНЧШ§НЧаЮЃЌ
дђжБЯпBQЕФжБЯпНтЮіЪНЮЊyЃНЉ2x+8ЃЌ
Ёр![]() ЃЌПЩЧѓxЃН3ЛђxЃН4ЃЈЩсЃЉ
ЃЌПЩЧѓxЃН3ЛђxЃН4ЃЈЩсЃЉ
ЁрxЃН3ЃЛ
ЁрQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛ
ЃЈ4ЃЉСНИіКЭаГЕуЃЛ
AOЃН1ЃЌOCЃН2ЃЌ
ЩшA1ЃЈxЃЌyЃЉЃЌдђC1ЃЈx+2ЃЌyЉ1ЃЉЃЌO1ЃЈxЃЌyЉ1ЃЉЃЌ
ЂйЕБA1ЁЂC1дкХзЮяЯпЩЯЪБЃЌ
Ёр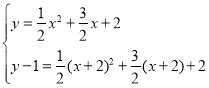 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁрA1ЕФКсзјБъЪЧ1ЃЛ
ЕБO1ЁЂC1дкХзЮяЯпЩЯЪБЃЌ
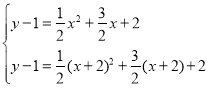 ЃЌЁр
ЃЌЁр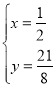 ЃЌ
ЃЌ
ЁрA1ЕФКсзјБъЪЧ![]() .
.