题目内容
解方程:
+
+
+…
=
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)•n |
| 2013 |
| 2014 |
考点:解分式方程
专题:计算题
分析:分式方程利用拆项法变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:方程变形得:1-
+
-
+…+
-
=
,即1-
=
,
去分母得:2014n-2014=2013n,
解得:n=2014,
经检验n=2014是分式方程的解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 2013 |
| 2014 |
| 1 |
| n |
| 2013 |
| 2014 |
去分母得:2014n-2014=2013n,
解得:n=2014,
经检验n=2014是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
 如图,将一个含有45°角的直角三角尺放在两条平行线m、n上,已知∠α=120°,则∠β的度数是( )
如图,将一个含有45°角的直角三角尺放在两条平行线m、n上,已知∠α=120°,则∠β的度数是( )| A、45° | B、60° |
| C、65° | D、75° |
 一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?
一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?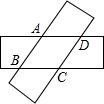 如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由.
如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE. 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D.
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及y=x+1的图象分别交于点C、D. 如图,在正方形ABCD中,E是边CD的中点.
如图,在正方形ABCD中,E是边CD的中点.