Question

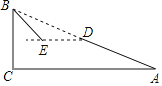
【题目】如图，斜坡AB长130米，坡度i=1：2.4，BC⊥AC，

（1）BC= m，AC= m；

（2）现在计划在斜坡AB的中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE，若斜坡BE的坡角为30°，求平台DE的长；（精确到0.1米，参考数据：≈1.41，≈1.73，≈2.45）

Answer 1

【答案】（1）BC=50m，AC=120m；（2）平台DE的长约为16.8m

【解析】

（1）直接利用坡比的定义结合勾股定理得出BC，AC的长；

（2）求得出BF，DF的长，然后在直角△BEF中利用三角函数求得EF的长，即可得出答案．

（1）∵AB长130米，坡度i=1：2.4，

∴设BC=xm，AC=2.4xm，

则x2+（2.4x）2=1302，

解得：x=50，

则2.4x=120m，

故BC=50m，AC=120m．

（2）延长DE到BC于点F，

∵D为AB的中点，

∴可得F是BC的中点，

∴BF=25m，

∴DF=25×2.4=60（m），

∵∠BEF=30°，

∴EF=，

∴DE=DF-EF=60-25≈16.8，

答：平台DE的长约为16.8米．